Question

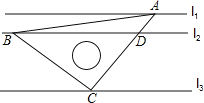
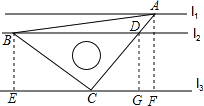
【题目】如图，直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为3．把一块含有45°角的直角三角板如图所示放置，顶点A，B，C恰好分别落在三条直线上，AC与直线l2交于点D，则线段BD的长度为_____．

Answer 1

【答案】

【解析】

分别过点A、B、D作AF⊥l3，BE⊥l3，DG⊥l3，先根据全等三角形的判定定理得出△BCE≌△ACF，故可得出CF及CE的长，在Rt△ACF中根据勾股定理求出AC的长，再由相似三角形的判定得出△CDG∽△CAF，故可得出CD的长，在Rt△BCD中根据勾股定理即可求出BD的长．

解：别过点A、B、D作AF⊥l3，BE⊥l3，DG⊥l3，

∵△ABC是等腰直角三角形，

∴AC＝BC，

∵∠EBC+∠BCE＝90°，∠BCE+∠ACF＝90°，∠ACF+∠CAF＝90°，

∴∠EBC＝∠ACF，∠BCE＝∠CAF，

在△BCE与△ACF中，

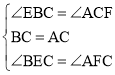
∴△BCE≌△ACF（ASA）

∴CF＝BE，CE＝AF，

∵l1与l2的距离为1，l2与l3的距离为3，

∴CF＝BE＝3，CE＝AF＝3+1＝4，

在Rt△ACF中，

∵AF＝4，CF＝3，

∴AC＝5，

∵AF⊥l3，DG⊥l3，

∴△CDG∽△CAF，

，

，

，

在Rt△BCD中，

∵，BC＝5，

所以．

故答案为：．