Question

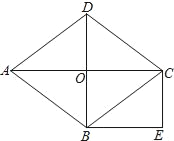
【题目】如图，O是菱形ABCD对角线AC与BD的交点，CD=5cm，OD=3cm；过点C作CE∥DB，过点B作BE∥AC，CE与BE相交于点E．

（1）求OC的长；

（2）求四边形OBEC的面积．

Answer 1

【答案】（1）OC=4cm；（2）S矩形OBEC= 12cm2．

【解析】分析：（1）在直角△OCD中，利用勾股定理即可求解；
（2）利用矩形的定义即可证明，再利用矩形的面积公式即可直接求解．

详解：

（1）∵ABCD是菱形，

∴AC⊥BD，

∴直角△OCD中，OC=（cm）；

（2）∵CE∥DB，BE∥AC，

∴四边形OBEC为平行四边形，

又∵AC⊥BD，即∠COB=90°，

∴平行四边形OBEC为矩形，

∵OB=0D，

∴S矩形OBEC=OBOC=4×3=12（cm2）．