题目内容
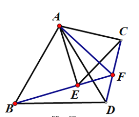
【题目】如图,等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,下列结论:(1)BE=CD ;(2)AF平分∠EAC ; (3)∠BFD=60°;(4)AF+FD=BF 其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
(1)先证△BAE≌△DAC,即可得到BE=CD;
(2)利用四点共圆的判定证出A、E、F、C四点共圆,再利用反证法假设(2)成立得到与条件矛盾即可说明假设不成立;
(3)根据A、E、F、C四点共圆,可求出∠EFC,然后就可求∠BFD;
(4)利用截长补短法:在BF上找到点G使得FG=FA,先证△AFG是等边三角形,再证
△BAG≌△DAF即可证出结论.
在BF上找到点G使得FG=FA,如下图所示:
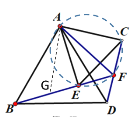
∵△ABD和△ACE是等边三角形
∴∠BAD=∠EAC=60°,AB=AD,AE=AC
∴∠BAD-∠EAD=∠EAC-∠EAD
∴∠BAE=∠DAC,
在△BAE和△DAC中,

∴△BAE≌△DAC,(SAS)
∴BE=CD,故(1)正确;
∠BEA=∠ACD,
∵∠AEB+∠AEF=180°,
∴∠AEF+∠ACF=180°,
∴A、E、F、C四点共圆,
∴假设(2)正确,即∠EAF=∠CAF
由圆的性质可得EF=FC
∴∠FEC=∠FCE
∴∠FEC+∠AEC=∠FCE+∠ACE
∴∠AEF=∠ACF
又∵∠AEF+∠ACF=180°(已证)
∴∠AEF=∠ACF=90°
而题中的∠AEF是动角,不一定是90°,矛盾,
故(2)不一定正确;
∵A、E、F、C四点共圆,∠EAC=60°
∴∠EFC=120°,
∴∠BFD=180°-∠EFC =60°,故(3)正确;
∵AE=AC,
∴∠AFC=∠AFE=![]() ∠EFC=60°
∠EFC=60°
∵FG=FA,
∴△AFG是等边三角形,
∴AG=AF,∠FAG=60°
∵∠BAG+∠GAD=60°,∠FAD+∠GAD =60°,
∴∠BAG =∠FAD,
在△BAG和△DAF中,
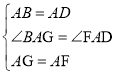
∴△BAG≌△DAF(SAS),
∴BG=FD,
∴AF+FD=FG+BG=BF,故(4)正确;
∴正确的结论有3个.
故选C.