Question

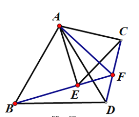
【题目】已知:如图， △ABC中，AB=AC,D在AC上,E在BC上，A E,B D交于F,∠AFD=60°，∠FDC+∠FEC=180°.

(1)求证：BE=CD.

(2)如图2，过点D作DG⊥AF于G，直接写出AE ，FG, BF的关系.

(3)如图3，在(2)的条件下,连接CG,若FG=BF，△AGD的面积等于5，求GC的长度.

Answer 1

【答案】（1）见详解；（2）AE－BF=2FG；（3）

【解析】

（1）证明△ABE≌△BCD即可；

（2）利用△ABE≌△BCD，可得AE=BD，由图可知DF=BD－BF，再利用30°所对的直角边是斜边的一半，可得DF=2GF，即可得到AE，FG,BF的关系；

（3）连接BG，将三角形CBG绕点C顺时针旋转，是CB与CA重合，G点落在M处连接GM，先利用条件证出△GCM为等边三角形，再证出△GAM为等腰直角三角形，利用

△AGD的面积等于5，求出GA2，最后利用勾股定理求出GM即为GC.

解：（1）∵∠FDC+∠FEC=180°，∠FEC+∠AEB=180°

∴∠FDC=∠AEB

∵AB=AC

∴∠ABC=∠ACB

∵∠BAE=180°―∠ABC―∠AEB

∠CBD=180°―∠ACB―∠FDC

∴∠BAE=∠CBD

∵∠AFD是△ABF的外角

∴∠AFD=∠BAE＋∠ABF=∠CBD＋∠ABF=∠ABC

∴∠ABC=60°

∴△ABC是等边三角形

∴AB=BC

在△ABE和△BCD中

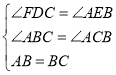
∴△ABE≌△BCD（AAS）

∴BE=CD

（2）∵△ABE≌△BCD

∴AE=BD

在Rt△GFD中∵∠GFD=60°

∴∠GDF=30°

∴

∴BD－BF=2FG

∴AE－BF=2FG

（3）连接BG，将三角形CBG绕点C顺时针旋转，是CB与CA重合，G点落在M处连接GM.

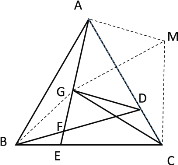
可得BG=AM，CG=CM，∠GBC=∠MAC，∠GCB=∠MCA

∴∠MCG=∠MCA＋∠ACG=∠GCB＋∠ACG=∠ACB=60°

∴△GCM为等边三角形

∴CG=CM=GM

∵FG=BF，∠GFD是△FBG的外角

∴∠FBG=∠FGB=∠GFD=30°

又∵∠GDF=30°

∴GB=GD，∠BGD=120°

又∵∠BAD=60°

∴点A在以G为圆心，GB为半径的圆上

∴GB=GD=GA，△AGD的面积等于5

∴∠GAB=∠GBA=∠FGB=15°，GD·GA=5

∴GA2=10

由（1）中△ABE≌△BCD

∴∠DBC=∠GAB=15°

∴∠GBC=∠FBG＋∠DBC=45°

∴∠CAM=45°

∴∠GAM=90°

∴△GAM为等腰直角三角形，

∴GM=

∴GC=GM=