题目内容
【题目】如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2016C2017B的面积为_____.

【答案】![]()
【解析】
矩形ABCD的面积=AB×AD=1,过点O向AB作垂线,垂足为E,平行四边形AOC1B的面积=AB×OE,根据矩形的性质,OE=![]() AD,即平行四边形AOC1B的面积=AB×
AD,即平行四边形AOC1B的面积=AB×![]() AD=
AD=![]() ,过点O1向AB作垂线,垂足为F,根据平行四边形的性质,O1F=
,过点O1向AB作垂线,垂足为F,根据平行四边形的性质,O1F=![]() OE=
OE=![]() AD,即平行四边形AO1C2B面积=AB×
AD,即平行四边形AO1C2B面积=AB×![]() AD=
AD=![]() ,依此类推,即可得到平行四边形AO2016C2017B的面积.
,依此类推,即可得到平行四边形AO2016C2017B的面积.
解:过点O向AB作垂线,垂足为E,过点O1向AB作垂线,垂足为F,如下图所示:
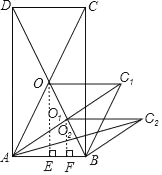
∵∠DAB=∠OEB,
∴OE∥DA,
∵O为矩形ABCD的对角线交点,
∴OB=OD
∴OE=![]() AD,
AD,
矩形ABCD的面积=AB×AD=1,
平行四边形AOC1B的面积=AB×OE=AB×![]() AD=
AD=![]() ,
,
同理,根据平行四边形的性质,
O1F=![]() OE=
OE=![]() AD,
AD,
平行四边形AO1C2B面积=AB×![]() AD=
AD=![]() ,
,
依此类推:
平行四边形AO2016C2017B的面积=AB×![]() AD=
AD=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目