Question

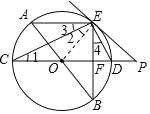
【题目】如图，AB、CD为⊙O的直径，弦AE∥CD，连接BE交CD于点F，过点E作直线EP与CD的延长线交于点P，使∠PED＝∠C．

（1）求证：PE是⊙O的切线；

（2）求证：DE平分∠BEP；

（3）若⊙O的半径为10，CF＝2EF，求BE的长．

Answer 1

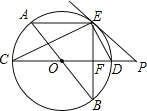
【答案】（1）见解析；（2）见解析；（3）BE＝16．

【解析】

（1）如图，连接OE．欲证明PE是⊙O的切线，只需推知OE⊥PE即可；

（2）由圆周角定理得到 ，根据“同角的余角相等”推知 ，结合已知条件证得结论；

（3）设 ，则 ，由勾股定理可求EF的长，即可求BE的长．

（1）如图，连接OE．

∵CD是圆O的直径，

∴ ．

∵ ，

∴ ．

又∵ ，即 ，

∴ ，

∴ ，即 ，

∴ ，

又∵点E在圆上，

∴PE是⊙O的切线；

（2）∵AB、CD为⊙O的直径，

∴ ，

∴ （同角的余角相等）．

又∵ ，

∴ ，

即ED平分∠BEP；

（3）设 ，则 ，

∵⊙O的半径为10，

∴ ，

在Rt△OEF中， ，即 ，

解得 ，

∴ ，

∴ ．