题目内容
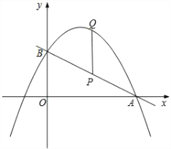
【题目】如图,直线y1=kx+2与x轴交于点A(m,0)(m>4),与y轴交于点B,抛物线y2=ax2﹣4ax+c(a<0)经过A,B两点.P为线段AB上一点,过点P作PQ∥y轴交抛物线于点Q.
(1)当m=5时,
①求抛物线的关系式;
②设点P的横坐标为x,用含x的代数式表示PQ的长,并求当x为何值时,PQ=![]() ;
;
(2)若PQ长的最大值为16,试讨论关于x的一元二次方程ax2﹣4ax﹣kx=h的解的个数与h的取值范围的关系.
【答案】(1)①y=﹣![]() x2+
x2+![]() x+2;②当x=1或x=4时,PQ=
x+2;②当x=1或x=4时,PQ=![]() ;
;
(2)当h=16时,一元二次方程ax2﹣4ax﹣kx=h有两个相等的实数解;
当h>16时,一元二次方程ax2﹣4ax﹣kx=h没有实数解;
当0<h<16时,一元二次方程ax2﹣4ax﹣kx=h有两个解.
【解析】试题分析:(1)①有m=5得到A点坐标,再把A点坐标代入直线解析式求出k得到y1=﹣![]() x+2,接着计算自变量为0时对应的函数值可得B点坐标,然后把A点和B点坐标代入y2=ax2﹣4ax+c得到a和c的方程组,再解方程组求出a、c即可得到抛物线解析式;②利用二次函数图象上点的坐标特征和一次函数图象上点的坐标特征,设点P的坐标为(x,﹣
x+2,接着计算自变量为0时对应的函数值可得B点坐标,然后把A点和B点坐标代入y2=ax2﹣4ax+c得到a和c的方程组,再解方程组求出a、c即可得到抛物线解析式;②利用二次函数图象上点的坐标特征和一次函数图象上点的坐标特征,设点P的坐标为(x,﹣![]() x+2),Q(x,﹣
x+2),Q(x,﹣![]() x2+
x2+![]() x+2),则可表示出PQ=﹣
x+2),则可表示出PQ=﹣![]() x2+2x,然后利用PQ=
x2+2x,然后利用PQ=![]() 得到﹣
得到﹣![]() x2+2x=
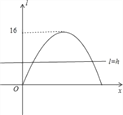
x2+2x=![]() ,然后解方程即可;(2)设P(x,kx+2),则Q(x,ax2﹣4ax+2),PQ的长用l表示,则易得l=ax2﹣(4a+k)x,再利用PQ长的最大值为16大致画出l与x的二次函数图象,由于一元二次方程ax2﹣4ax﹣kx=h的解的情况可看作为二次函数l=ax2﹣4ax﹣kx与直线l=h的交点个数,则利用函数图象可判断当h=16时,一元二次方程ax2﹣4ax﹣kx=h有两个相等的实数解;当h>16时,一元二次方程ax2﹣4ax﹣kx=h没有实数解;当0<h<16时,一元二次方程ax2﹣4ax﹣kx=h有两个解.
,然后解方程即可;(2)设P(x,kx+2),则Q(x,ax2﹣4ax+2),PQ的长用l表示,则易得l=ax2﹣(4a+k)x,再利用PQ长的最大值为16大致画出l与x的二次函数图象,由于一元二次方程ax2﹣4ax﹣kx=h的解的情况可看作为二次函数l=ax2﹣4ax﹣kx与直线l=h的交点个数,则利用函数图象可判断当h=16时,一元二次方程ax2﹣4ax﹣kx=h有两个相等的实数解;当h>16时,一元二次方程ax2﹣4ax﹣kx=h没有实数解;当0<h<16时,一元二次方程ax2﹣4ax﹣kx=h有两个解.
试题解析:
(1)①∵m=5,∴点A的坐标为(5,0),
把A(5,0)代入y1=kx+2得5k+2=0,解得k=﹣![]() ,∴直线解析式为y1=﹣
,∴直线解析式为y1=﹣![]() x+2,
x+2,
当x=0时,y1=2,∴点B的坐标为(0,2).
将A(5,0),B(0,2)代入![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴抛物线的表达式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
②设点P的坐标为(x,﹣![]() x+2),则Q(x,﹣
x+2),则Q(x,﹣![]() x2+
x2+![]() x+2),
x+2),
∴PQ=﹣![]() x2+
x2+![]() x+2﹣(﹣
x+2﹣(﹣![]() x+2)=﹣
x+2)=﹣![]() x2+2x,而PQ=
x2+2x,而PQ=![]() ,
,
∴﹣![]() x2+2x=
x2+2x=![]() ,解得:x1=1,x2=4,∴当x=1或x=4时,PQ=
,解得:x1=1,x2=4,∴当x=1或x=4时,PQ=![]() ;
;
(2)设P(x,kx+2),则Q(x,ax2﹣4ax+2),PQ的长用l表示,
∴l=ax2﹣4ax+2﹣(kx+2)=ax2﹣(4a+k)x,∵PQ长的最大值为16,如图,
当h=16时,一元二次方程ax2﹣4ax﹣kx=h有两个相等的实数解;
当h>16时,一元二次方程ax2﹣4ax﹣kx=h没有实数解;
当0<h<16时,一元二次方程ax2﹣4ax﹣kx=h有两个解.

【题目】某实验中学为了进一步丰富学生的课余生活,拟调整兴趣活动小组,为此进行了一次调查,结果如下,请看表回答:
选项 | 美术 | 电脑 | 音乐 | 体育 |
占调查人数的百分率 | 15% | 30% | 30% |
(1)喜欢体育项目的人数占总体的百分比是多少?
(2)表示“电脑”部分的圆心角是多少度?
(3)根据所给数据,画出表示调查结果的扇形统计图.