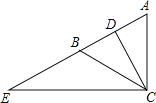
Ő‚ńŅńŕ»›
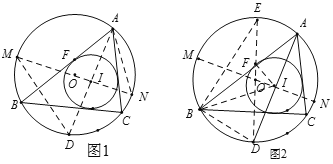
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘ŕĶ»ĪŖ![]() ÷–£¨
÷–£¨![]() £¨∂ĮĶ„
£¨∂ĮĶ„![]() ī”Ķ„
ī”Ķ„![]() ≥Ų∑Ę“‘
≥Ų∑Ę“‘![]() ĶńňŔ∂»—ō
ĶńňŔ∂»—ō![]() ‘»ňŔ‘ň∂Į£¨∂ĮĶ„
‘»ňŔ‘ň∂Į£¨∂ĮĶ„![]() Õ¨ Īī”Ķ„
Õ¨ Īī”Ķ„![]() ≥Ų∑Ę“‘Õ¨—ýĶńňŔ∂»—ō
≥Ų∑Ę“‘Õ¨—ýĶńňŔ∂»—ō![]() Ķń—”≥§ŌŖ∑ĹŌÚ‘»ňŔ‘ň∂Į£¨ĶĪĶ„
Ķń—”≥§ŌŖ∑ĹŌÚ‘»ňŔ‘ň∂Į£¨ĶĪĶ„![]() ĶĹīÔĶ„
ĶĹīÔĶ„![]() Ī£¨Ķ„
Ī£¨Ķ„![]() °Ę
°Ę![]() Õ¨ ĪÕ£÷Ļ‘ň∂Į£ģ…Ť‘ň∂Į Īľšő™
Õ¨ ĪÕ£÷Ļ‘ň∂Į£ģ…Ť‘ň∂Į Īľšő™![]() £¨ĻżĶ„
£¨ĻżĶ„![]() ◊ų
◊ų![]() ”ŕ
”ŕ![]() £¨
£¨![]() ĹĽ
ĹĽ![]() ĪŖ”ŕ
ĪŖ”ŕ![]() £¨ŌŖ∂ő
£¨ŌŖ∂ő![]() Ķń÷–Ķ„ő™
Ķń÷–Ķ„ő™![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £ģ
£ģ
£®1£©ĶĪ![]() ő™ļő÷Ķ Ī£¨
ő™ļő÷Ķ Ī£¨![]() ”Ž
”Ž![]() Ōŗň∆£Ľ
Ōŗň∆£Ľ
£®2£©‘ŕĶ„![]() °Ę
°Ę![]() ‘ň∂ĮĻż≥Ő÷–£¨Ķ„
‘ň∂ĮĻż≥Ő÷–£¨Ķ„![]() °Ę
°Ę![]() “≤ňś÷ģ‘ň∂Į£¨ŌŖ∂ő
“≤ňś÷ģ‘ň∂Į£¨ŌŖ∂ő![]() Ķń≥§∂» «∑ŮĽŠ∑Ę…ķĪšĽĮ£Ņ»Ű∑Ę…ķĪšĽĮ£¨«ŽňĶ√ųņŪ”…£¨»Ű≤Ľ∑Ę…ķĪšĽĮ£¨«ů
Ķń≥§∂» «∑ŮĽŠ∑Ę…ķĪšĽĮ£Ņ»Ű∑Ę…ķĪšĽĮ£¨«ŽňĶ√ųņŪ”…£¨»Ű≤Ľ∑Ę…ķĪšĽĮ£¨«ů![]() Ķń≥§£Ľ
Ķń≥§£Ľ
£®3£©»ÁÕľ2£¨Ĺę![]() —ō÷ĪŌŖ
—ō÷ĪŌŖ![]() ∑≠’Ř£¨Ķ√
∑≠’Ř£¨Ķ√![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨ĶĪ
£¨ĶĪ![]() ő™ļő÷Ķ Ī£¨
ő™ļő÷Ķ Ī£¨![]() Ķń÷Ķ◊Ó–°£Ņ≤Ę«ů≥Ų◊Ó–°÷Ķ£ģ
Ķń÷Ķ◊Ó–°£Ņ≤Ę«ů≥Ų◊Ó–°÷Ķ£ģ
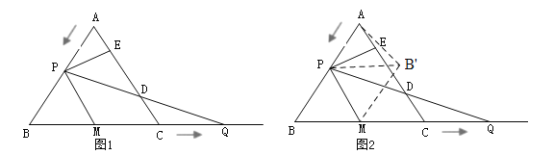
°ĺīūįł°Ņ£®1£©3£Ľ£®2£©≤ĽĪšĽĮ£¨3cm£Ľ£®3£©![]() £¨◊Ó–°÷Ķ
£¨◊Ó–°÷Ķ![]()
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›Ő‚“‚ĶĪ![]() £¨
£¨![]() £¨Ļ Ņ…«ůĹ‚£Ľ
£¨Ļ Ņ…«ůĹ‚£Ľ
£®2£©◊ų![]() ĹĽ
ĹĽ![]() ”ŕ
”ŕ![]() £¨Ķ√ĶĹ
£¨Ķ√ĶĹ![]() «Ķ»ĪŖ»żĹ«–ő£¨
«Ķ»ĪŖ»żĹ«–ő£¨![]() £¨AE=EK£¨‘Ŕ÷§√ų
£¨AE=EK£¨‘Ŕ÷§√ų![]() £¨Ķ√ĶĹ
£¨Ķ√ĶĹ![]() £¨ņŻ”√
£¨ņŻ”√![]() ľīŅ…«ůĹ‚£Ľ
ľīŅ…«ůĹ‚£Ľ
£®3£©Ń¨Ĺ”![]() £¨
£¨![]() £¨Ņ…Ķ√
£¨Ņ…Ķ√![]() ,”…
,”…![]() Ņ…÷™ĶĪ
Ņ…÷™ĶĪ![]() £¨
£¨![]() £¨
£¨![]() ‘ŕ“ĽŐű÷ĪŌŖ…Ō Ī£¨
‘ŕ“ĽŐű÷ĪŌŖ…Ō Ī£¨![]() ◊Ó–°£¨‘Ŕłýĺ›’ŘĶĢĶń–‘÷ ľįĻīĻ…∂®ņŪľīŅ…«ů≥Ų
◊Ó–°£¨‘Ŕłýĺ›’ŘĶĢĶń–‘÷ ľįĻīĻ…∂®ņŪľīŅ…«ů≥Ų![]() Ķń◊Ó–°÷Ķ.
Ķń◊Ó–°÷Ķ.
Ĺ‚£ļ£®1£©![]() «Ķ»ĪŖ»żĹ«–ő£¨
«Ķ»ĪŖ»żĹ«–ő£¨
°ŗ![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
°ŗ÷Ľ”–ĶĪ![]() Ī,
Ī,![]() ,
,
‘Ú![]() £¨
£¨![]() «
«![]() Ķń÷–Ķ„£¨
Ķń÷–Ķ„£¨
![]() «
«![]() Ķń÷–Ķ„£¨
Ķń÷–Ķ„£¨
ľī![]() ,
,
![]() Ī£¨
Ī£¨![]() £Ľ
£Ľ
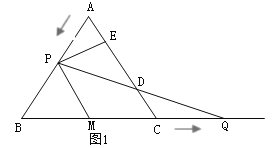
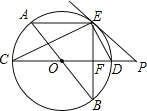
£®2£©≤ĽĪšĽĮ.ņŪ”…»ÁŌ¬£ļ
»ÁÕľ2÷–£¨◊ų![]() ĹĽ
ĹĽ![]() ”ŕ
”ŕ![]() .
.
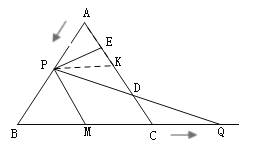
![]() «Ķ»ĪŖ»żĹ«–ő£¨
«Ķ»ĪŖ»żĹ«–ő£¨
![]() £¨
£¨
![]() £¨
£¨
![]() ,
,
![]() «Ķ»ĪŖ»żĹ«–ő£¨
«Ķ»ĪŖ»żĹ«–ő£¨
![]() £¨
£¨
![]() £¨
£¨
°ŗAE=EK£¨
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]()
£®3£©»ÁÕľ3÷–£¨Ń¨Ĺ”![]() £¨
£¨![]() £¨
£¨
‘Ú![]() ,
,
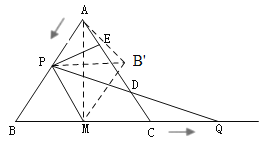
∂Ý![]() £¨
£¨
°ŗĶĪ![]() £¨
£¨![]() £¨
£¨![]() ‘ŕ“ĽŐű÷ĪŌŖ…Ō Ī£¨
‘ŕ“ĽŐű÷ĪŌŖ…Ō Ī£¨![]() ◊Ó–°£¨
◊Ó–°£¨
![]() £¨
£¨![]() £¨
£¨
![]() ,
,
![]() £¨
£¨
![]() £¨
£¨
![]() Ķń◊Ó–°÷Ķő™
Ķń◊Ó–°÷Ķő™![]() .
.

 ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł –°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
–°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł