题目内容
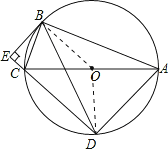
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AC=13,BC=5,BE⊥DC交DC的延长线于点E.

(1)求证:CB是∠ECA的角平分线;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
【答案】(1)证明见解析;(2)![]() .(3)证明见解析.
.(3)证明见解析.
【解析】
试题分析:(1)根据BD=BA得出∠BDA=∠BAD,再由∠BCA=∠BDA即可得出结论;
(2)判断△BED∽△CBA,利用对应边成比例的性质可求出DE的长度.
(3)连接OB,OD,证明△ABO≌△DBO,推出OB∥DE,继而判断BE⊥OB,可得出结论.
试题解析:(1)∵BD=BA,
∴∠BDA=∠BAD,
∵∠BCA=∠BDA,
∴∠BCA=∠BAD.
∴CB是∠ECA的角平分线;
(2)∵∠BDE=∠CAB且∠BED=∠CBA=90°,
∴△BED∽△CBA,
∴![]() ,
,
由勾股定理易求AB=12.
即![]() ,
,
解得:DE=![]() .
.
(3)连结OB,OD,
在△ABO和△DBO中,
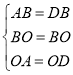 ,
,
∴△ABO≌△DBO(SSS),
∴∠DBO=∠ABO,
∵∠ABO=∠OAB=∠BDC,
∴∠DBO=∠BDC,
∴OB∥ED,
∵BE⊥ED,
∴EB⊥BO,
∴BE是⊙O的切线.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目