题目内容
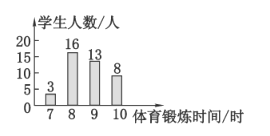
【题目】某校为了了解学生使用手机情况,随机抽取了部分学生进行|使用手机的目的和每周使用手机的时间的问卷调查,并绘制成如图所示的统计图,已知“查资料”的人数为38人。
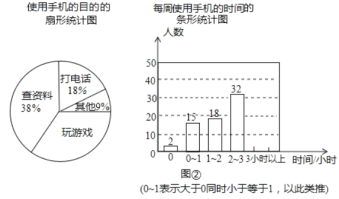
根据以上信息,回答下列问题:
(1)这次调查中,一共抽查了__________名学生;
(2)在扇形统计图中,“玩游戏”所对应的圆心角的度数是___________度;
(3)补全条形统计图;
(4)若该校共有学生2000人,请你估计每周使用手机时间超过2小时的人数.
【答案】(1)100;(2)126;(3)见解析;(4)1300人.
【解析】
(1)根据查资料的人数和所占的百分比可以求得本次调查的总人数;
(2)根据扇形统计图中的数据求出“玩游戏”所占比例,进而求出所对应的圆心角的度数;
(3)根据(1)中的结果和条形统计图中的数据可以求得使用手机3小时以上的人数,从而可以将条形统计图补充完整;
(4)利用样本估计总体的思想计算即可.
解:(1)在这次调查中,一共抽取了38÷38%=100名学生,
故答案为:100;
(2)在扇形统计图中,“玩游戏”所对应的圆心角的度数是360°×(138%18%9%)=126°,
故答案为:126;
(3)使用手机3小时以上的人数为:1002151832=33,
补全条形统计图如图所示:

(4)2000×![]() =1300(人),
=1300(人),
答:估计每周使用手机时间超过2小时的人数有1300人.

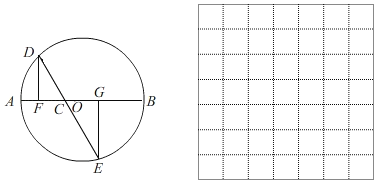
【题目】如图,AB是⊙O的直径,AB=4cm,C为AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=60°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=xcm,DE=ycm(当x的值为0或3时,y的值为2),探究函数y随自变量x的变化而变化的规律.
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:点F与点O重合时,DE长度约为 cm(结果保留一位小数).