题目内容
【题目】如图，在平面直角坐标系
中，点A的坐标为A(1，0)，等腰直角三角形ABC的边AB在x轴的正半轴上，∠ABC＝90°，点B在点A的右侧，点C在第一象限．将△ABC绕点A逆时针旋转
，
（1）若＝75°，如果点C的对应点E恰好落在
轴的正半轴上，求AB的长；
（2）若旋转°后，有DE∥AC，且点B的对应点D也恰好落在轴的正半轴上，求DC的长．
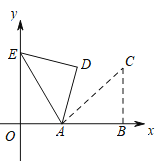
【答案】（1）
；（2）
【解析】
（1）依据旋转的性质，即可得到∠OAE＝60°，再根据OA＝1，∠EOA＝90°，∠OAE＝60°，即可得出AE＝2，AC＝2．最后在Rt△ABC中，可得到
．
（2）当
时， 
，画出图形，根据等腰直角三角形的特点求得C、D两点的坐标，再根据勾股定理求得DC的长度
（1）依题意得：
，
，
，
，
，
，
．
（2）当时， ，
且点B的对应点D也恰好落在y轴的正半轴上时，
OA=OD=1，AB=CB=，
∴D（0，1），C（1+，），
∴
．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
