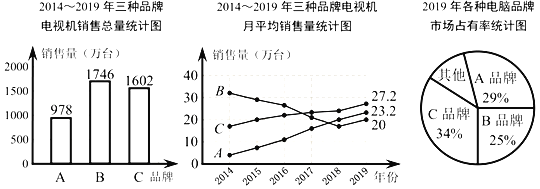
��Ŀ����
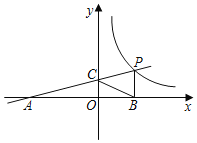
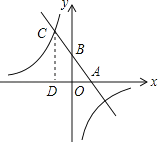
����Ŀ����ƽ��ֱ������ϵxoy�У�ֱ��y��4x+4�ֱ���x �� ��y ��ֱ���A��B����A��������y��ax2+bx��3a (a��0)�ϣ�����B����ƽ��3����λ���ȣ��õ���C��
��1���������ߵĶ������ꣻ���ú�a�Ĵ���ʽ��ʾ��
��2����a=��1����t��1��x��tʱ������y��ax2+bx��3a (a��0)�����ֵ��3����t��ֵ��
��3�������������߶�BC�����������㣬��Ϻ���ͼ��ֱ��д��a��ȡֵ��Χ��
���𰸡���1����1����4a������2��t��0�� t��3����3����![]() ��a����1��
��a����1��
��������
��1����![]() ���������ߵ�
���������ߵ�![]() ���ٽ������߽���ʽ��Ϊ����ʽ������⣻
���ٽ������߽���ʽ��Ϊ����ʽ������⣻
��2����![]() ʱ�������߶�������Ϊ
ʱ�������߶�������Ϊ![]() ��Ȼ���������������ߵ����ʿɽ��
��Ȼ���������������ߵ����ʿɽ��
��3�������B���꣬����B����ƽ��3����λ���ȣ��õ���C�����������ߵĶ���������⣮
�⣺��1��ֱ��y��4x+4��x�ᣬy��ֱ��ڵ�A��B��
��![]() ��
��![]() ��
��
��A��������y��ax2+bx��3a (a��0)�ϣ�
��![]() ��
��
��������![]() ��
��
�������ߵĶ�������Ϊ��1����4a����
��2����a����1��
��������y����x2+2x+3������x��1��2+4��
��![]() ʱ��
ʱ��![]() ��
��
��ã�![]() ��
��![]() ����ȥ����
����ȥ����
��![]() ʱ����
ʱ����![]() ��
��![]() ��
��
��ã�![]() ����ȥ����
����ȥ����![]() ��
��
���������ɵã�t��0�� t��3��
��3���ٰ�![]() ���������ߣ��õ�
���������ߣ��õ�![]() ��
��
�������ߵĶ��㲻���߶�BC��ʱ�����������߶����������㣬
��![]() ��
��
��![]()
�ڵ������ߵĶ������߶�BC��ʱ��������Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
��a��ȡֵ��Χ�ǩ�![]() ��a����1��
��a����1��

����Ŀ��Ϊ��һ������ѧ���ķ������ʣ���ѧ��֯ѧ����չ���ܷ���֪ʶ��������ѧУ�����ȡ����ѧ���ijɼ�������ͳ�Ʒ��������˽�ѧ���ķ���֪ʶˮƽ��������Щѧ���ľ����ɼ��ֲ�������������ɼ���Ϊ�ס��ҡ���������������ȼ���ͼ�����£�
�ȼ� | ����/�� | Ƶ�� | �����ܷ�/�� |
�� |
| 39 | 2184 |
�� |
| 75 | 5175 |
�� |
| 120 | 9720 |
�� |
|
| 4050 |
�� |
| 21 | 2037 |

��1����![]() ��ֵ��
��ֵ��
��2�������ɼ�����λ�������ĸ��ȼ���
��3�������龺���ɼ���ƽ��ֵ��