ĚâÄżÄÚČÝ
ĄžĚâÄżĄżÔÚĆ˝ĂćÖą˝Ç×řąęĎľxOyÖĐŁŹľăPÓëľăQ˛ťÖغϣŹŇÔľăPÎŞÔ˛ĐÄ×÷žšýQľÄÔ˛ŁŹÔňłĆ¸ĂԲΪľăPĄ˘QľÄĄ°ĎŕšŘÔ˛Ąą 
Ł¨1ŁŠŇŃÖŞľăPľÄ×řąęÎŞŁ¨2ŁŹ0ŁŠ ˘ŮČôľăQľÄ×řąęÎŞŁ¨0ŁŹ1ŁŠŁŹÇóľăPĄ˘QľÄĄ°ĎŕšŘÔ˛ĄąľÄĂćťýŁť
˘ÚČôľăQľÄ×řąęÎŞŁ¨3ŁŹnŁŠŁŹÇŇľăPĄ˘QľÄĄ°ĎŕšŘÔ˛ĄąľÄ°ëžśÎŞ ![]() ŁŹÇónľÄÖľŁť
ŁŹÇónľÄÖľŁť
Ł¨2ŁŠŇŃÖŞĄ÷ABCÎŞľČąßČý˝ÇĐÎŁŹľăAşÍľăBľÄ×řąęˇÖąđÎŞŁ¨Š ![]() ŁŹ0ŁŠĄ˘Ł¨
ŁŹ0ŁŠĄ˘Ł¨ ![]() ŁŹ0ŁŠŁŹľăCÔÚyÖáŐý°ëÖáÉĎŁŹČôľăPĄ˘QľÄĄ°ĎŕšŘÔ˛ĄąÇĄşĂĘÇĄ÷ABCľÄÄÚÇĐÔ˛ÇŇľăQÔÚÖąĎßy=2xÉĎŁŹÇóľăQľÄ×řąęŁŽ
ŁŹ0ŁŠŁŹľăCÔÚyÖáŐý°ëÖáÉĎŁŹČôľăPĄ˘QľÄĄ°ĎŕšŘÔ˛ĄąÇĄşĂĘÇĄ÷ABCľÄÄÚÇĐÔ˛ÇŇľăQÔÚÖąĎßy=2xÉĎŁŹÇóľăQľÄ×řąęŁŽ
Ł¨3ŁŠŇŃÖŞĄ÷ABCČý¸öśĽľăľÄ×řąęÎŞŁşAŁ¨Š3ŁŹ0ŁŠĄ˘BŁ¨ ![]() ŁŹ0ŁŠŁŹCŁ¨0ŁŹ4ŁŠŁŹľăPľÄ×řąęÎŞŁ¨0ŁŹ
ŁŹ0ŁŠŁŹCŁ¨0ŁŹ4ŁŠŁŹľăPľÄ×řąęÎŞŁ¨0ŁŹ ![]() ŁŠŁŹľăQľÄ×řąęÎŞŁ¨mŁŹ
ŁŠŁŹľăQľÄ×řąęÎŞŁ¨mŁŹ ![]() ŁŠŁŹČôľăPĄ˘QľÄĄ°ĎŕšŘÔ˛ĄąÓëĄ÷ABCľÄČýąßÖĐÖÁÉŮŇťąß´ćÔÚšŤš˛ľăŁŹÖą˝ÓĐ´łömľÄČĄÖľˇśÎ§ŁŽ
ŁŠŁŹČôľăPĄ˘QľÄĄ°ĎŕšŘÔ˛ĄąÓëĄ÷ABCľÄČýąßÖĐÖÁÉŮŇťąß´ćÔÚšŤš˛ľăŁŹÖą˝ÓĐ´łömľÄČĄÖľˇśÎ§ŁŽ
Ąž´đ°¸Ąż
Ł¨1ŁŠ˝âŁş˘ŮĄßPQ= ![]() =
= ![]() =
= ![]() ŁŹ
ŁŹ
ĄŕS=ŚĐr2=5ŚĐŁŽ
˘ÚšýľăQ×÷QHĄÍxÖáÓÚHŁŽ

ĄßHQ= ![]() =2ŁŹ
=2ŁŹ
ĄŕQľă×řąęÎŞŁ¨3ŁŹ2ŁŠťňŁ¨3ŁŹŠ2ŁŠŁŽ
Ąŕn=2ťňŠ2
Ł¨2ŁŠ˝âŁşČçÍźŁŹ
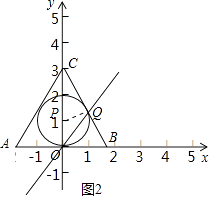
ÔÚRtĄ÷OACÖĐŁŹĄĎACO=30ĄăŁŹ
ĄŕOC= ![]() OA=3ŁŹ
OA=3ŁŹ
ĄŕCľă×řąęÎŞŁ¨0ŁŹ3ŁŠŁŹ
ĄŕĄ÷ABCľÄÄÚÇĐÔ˛ľÄÔ˛ĐÄľÄ×řąęÎŞŁ¨0ŁŹ1ŁŠŁŹ°ëžśÎŞ1ŁŹ
ĄŕPŁ¨0ŁŹ1ŁŠŁŹ
ÉčQŁ¨xŁŹ2xŁŠŁŹÔňÓĐx2+Ł¨2xŠ1ŁŠ2=1ŁŹ
˝âľĂx= ![]() ŁŹ
ŁŹ
ĄŕQŁ¨ ![]() ŁŹ
ŁŹ ![]() ŁŠ
ŁŠ
Ł¨3ŁŠ˝âŁşČçÍź3ÖĐŁŹ

˘ŮľąĎŕšŘÔ˛ÓëACĄ˘ABĎŕÇĐĘą°ëžśÓĐ×îĐĄÖľ ![]() ŁŽ
ŁŽ
˘ÚľąĎŕšŘÔ˛žšýľăBĘąŁŹ°ëžśÓĐ×î´óÖľ ![]() ŁŹ
ŁŹ
ĄŕŠ ![]() ĄÜmĄÜŠ
ĄÜmĄÜŠ ![]() ŁŹ
ŁŹ ![]() ĄÜmĄÜ
ĄÜmĄÜ ![]()
Ąž˝âÎöĄżŁ¨1ŁŠ˘Ů¸ůžÝPQ= ![]() =
= ![]() =
= ![]() ŁŹÇółöĄŃPľÄ°ëžśź´żÉ˝âžöÎĘĚ⣝˘ÚšýľăQ×÷QHĄÍxÖáÓÚHŁŽŔűÓĂš´šÉś¨ŔíÇółöQHľÄÖľŁŹź´żÉ˝âžöÎĘĚ⣝Ł¨2ŁŠÔÚRtĄ÷OACÖĐŁŹĄĎACO=30ĄăŁŹżÉľĂOC=
ŁŹÇółöĄŃPľÄ°ëžśź´żÉ˝âžöÎĘĚ⣝˘ÚšýľăQ×÷QHĄÍxÖáÓÚHŁŽŔűÓĂš´šÉś¨ŔíÇółöQHľÄÖľŁŹź´żÉ˝âžöÎĘĚ⣝Ł¨2ŁŠÔÚRtĄ÷OACÖĐŁŹĄĎACO=30ĄăŁŹżÉľĂOC= ![]() OA=3ŁŹÍĆłöCľă×řąęÎŞŁ¨0ŁŹ3ŁŠŁŹÍĆłöĄ÷ABCľÄÄÚÇĐÔ˛ľÄÔ˛ĐÄľÄ×řąęÎŞŁ¨0ŁŹ1ŁŠŁŹ°ëžśÎŞ1ŁŹÍĆłöPŁ¨0ŁŹ1ŁŠŁŹÉčQŁ¨xŁŹ2xŁŠŁŹÔňÓĐx2+Ł¨2xŠ1ŁŠ2=1ŁŹÇółöxź´żÉŁťŁ¨3ŁŠ˘ŮľąĎŕšŘÔ˛ÓëACĄ˘ABĎŕÇĐĘąŁŹżÉľĂ°ëžśÓĐ×îĐĄÖľ
OA=3ŁŹÍĆłöCľă×řąęÎŞŁ¨0ŁŹ3ŁŠŁŹÍĆłöĄ÷ABCľÄÄÚÇĐÔ˛ľÄÔ˛ĐÄľÄ×řąęÎŞŁ¨0ŁŹ1ŁŠŁŹ°ëžśÎŞ1ŁŹÍĆłöPŁ¨0ŁŹ1ŁŠŁŹÉčQŁ¨xŁŹ2xŁŠŁŹÔňÓĐx2+Ł¨2xŠ1ŁŠ2=1ŁŹÇółöxź´żÉŁťŁ¨3ŁŠ˘ŮľąĎŕšŘÔ˛ÓëACĄ˘ABĎŕÇĐĘąŁŹżÉľĂ°ëžśÓĐ×îĐĄÖľ ![]() ŁŽ˘ÚľąĎŕšŘÔ˛žšýľăBĘąŁŹżÉľĂ°ëžś×î´óÖľ
ŁŽ˘ÚľąĎŕšŘÔ˛žšýľăBĘąŁŹżÉľĂ°ëžś×î´óÖľ ![]() ŁŹÓÉ´Ëź´żÉ˝âžöÎĘĚ⣝
ŁŹÓÉ´Ëź´żÉ˝âžöÎĘĚ⣝

ĄžĚâÄżĄżÄłÉĚľęˇÖÁ˝´Îšş˝ř![]() Ą˘
Ą˘![]() Á˝ÖÖÉĚơ˝řĐĐĎúĘŰŁŹÁ˝´Îšş˝řÍŹŇťÖÖÉĚơľÄ˝řźŰĎŕÍŹŁŹžßĚĺÇéżöČçĎÂąíËůĘžŁş
Á˝ÖÖÉĚơ˝řĐĐĎúĘŰŁŹÁ˝´Îšş˝řÍŹŇťÖÖÉĚơľÄ˝řźŰĎŕÍŹŁŹžßĚĺÇéżöČçĎÂąíËůĘžŁş
šş˝řĘýÁżŁ¨źţŁŠ | šş˝řËůĐčˇŃÓĂŁ¨ÔŞŁŠ | ||
|
| ||
ľÚŇť´Î | 30 | 40 | 3800 |
ľÚśţ´Î | 40 | 30 | 3200 |
Ł¨1ŁŠÇó![]() Ą˘
Ą˘![]() Á˝ÖÖÉĚơÿźţľÄ˝řźŰˇÖąđĘÇśŕÉŮÔŞŁż
Á˝ÖÖÉĚơÿźţľÄ˝řźŰˇÖąđĘÇśŕÉŮÔŞŁż
Ł¨2ŁŠÉĚłĄžöś¨![]() ÖÖÉĚơŇÔĂżźţ30ÔŞłöĘŰŁŹ
ÖÖÉĚơŇÔĂżźţ30ÔŞłöĘŰŁŹ![]() ÖÖÉĚơŇÔĂżźţ100ÔŞłöĘŰŁŽÎŞÂú×ăĘĐłĄĐčÇóŁŹĐčšş˝ř
ÖÖÉĚơŇÔĂżźţ100ÔŞłöĘŰŁŽÎŞÂú×ăĘĐłĄĐčÇóŁŹĐčšş˝ř![]() Ą˘
Ą˘![]() Á˝ÖÖÉĚơš˛1000źţŁŹÇŇ
Á˝ÖÖÉĚơš˛1000źţŁŹÇŇ![]() ÖÖÉĚơľÄĘýÁż˛ťÉŮÓÚ
ÖÖÉĚơľÄĘýÁż˛ťÉŮÓÚ![]() ÖÖÉĚơĘýÁżľÄ4ąśŁŹÇëÄăÇółöťńŔű×î´óľÄ˝řťőˇ˝°¸ŁŹ˛˘Čˇś¨×î´óŔűČóŁŽ
ÖÖÉĚơĘýÁżľÄ4ąśŁŹÇëÄăÇółöťńŔű×î´óľÄ˝řťőˇ˝°¸ŁŹ˛˘Čˇś¨×î´óŔűČóŁŽ
ĄžĚâÄżĄżËć×ĹĄ°ťĽÁŞÍř+ĄąĘą´úľÄľ˝Ŕ´ŁŹŇťÖÖĐÂĐÍ´ňłľˇ˝Ę˝ĘÜľ˝´óÖÚťśÓŁŹ¸Ă´ňłľˇ˝Ę˝ľÄ×ܡŃÓĂÓÉŔďłĚˇŃşÍşÄĘąˇŃ×éłÉŁŹĆäÖĐŔďłĚˇŃ°´![]() ÔŞ/šŤŔďźĆË㣏şÄĘąˇŃ°´
ÔŞ/šŤŔďźĆË㣏şÄĘąˇŃ°´![]() ÔŞ/ˇÖÖÓźĆËă(×ܡŃÓòť×ă
ÔŞ/ˇÖÖÓźĆËă(×ܡŃÓòť×ă![]() ÔŞ°´
ÔŞ°´![]() ÔŞźĆźŰ)ŁŽĐĄĂôĄ˘ĐĄ¸ŐÁ˝ČËÓøôňłľˇ˝Ę˝łöĐĐŁŹ°´ÉĎĘöźĆźŰšćÔňŁŹĆäĐĐĘťŔďłĚĘýĄ˘şÄĘąŇÔź°´ňłľ×ܡŃÓĂČçĎÂąíŁş
ÔŞźĆźŰ)ŁŽĐĄĂôĄ˘ĐĄ¸ŐÁ˝ČËÓøôňłľˇ˝Ę˝łöĐĐŁŹ°´ÉĎĘöźĆźŰšćÔňŁŹĆäĐĐĘťŔďłĚĘýĄ˘şÄĘąŇÔź°´ňłľ×ܡŃÓĂČçĎÂąíŁş
ŔďłĚĘý | şÄĘą | łľˇŃ(ÔŞ) | |
ĐĄĂô |
|
|
|
ĐĄ¸Ő |
|
|
|
![]() Çó
Çó![]() ľÄÖľŁť
ľÄÖľŁť
![]() ČôĐĄťŞŇ˛Óøôňłľˇ˝Ę˝´ňłľŁŹĆ˝žůłľËŮÎŞ
ČôĐĄťŞŇ˛Óøôňłľˇ˝Ę˝´ňłľŁŹĆ˝žůłľËŮÎŞ![]() šŤŔď/ĘąŁŹĐĐĘťÁË
šŤŔď/ĘąŁŹĐĐĘťÁË![]()