题目内容
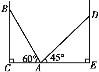
【题目】如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3 m.
(1)求两面墙之间距离CE的大小;
(2)求点B到地面的垂直距离BC的大小.
【答案】(1)两面墙之间的距离CE的大小为(3+3![]() )m;(2)点B到地面的垂直距离BC的大小为3
)m;(2)点B到地面的垂直距离BC的大小为3![]() m.
m.
【解析】
(1)在Rt△ADE中,运用勾股定理可求出梯子的总长度,然后利用勾股定理求得AC的长,从而求得线段CE的长;
(2)在Rt△ABC中,根据已知条件再次运用勾股定理可求出BC的长.
(1)在Rt△DAE中,
因为∠DAE=45°,DE=3![]() m,
m,
所以AE=DE=3![]() m,
m,
由勾股定理,得AD2=AE2+DE2=36,
所以AD=6 m,
即梯子的总长为6 m,所以AB=AD=6 m.
在Rt△ABC中,因为∠BAC=60°,
所以∠ABC=30°,所以AC=![]() AB=3 m,
AB=3 m,
所以CE=AC+AE=(3+3![]() )m,
)m,
所以两面墙之间的距离CE的大小为(3+3![]() )m.
)m.
(2)在Rt△ABC中,AB=6 m,AC=3 m,
由勾股定理,得
BC=![]() =
=![]() =
=![]() =3
=3![]() (m),
(m),
所以点B到地面的垂直距离BC的大小为3![]() m.
m.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目