题目内容
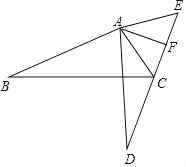
【题目】在△ABC中,BA=BC,BE平分∠ABC,CD⊥BD,且CD=BD.
(1)求证:BF=AC;
(2)若AD=![]() ,求CF的长.
,求CF的长.

【答案】(1)证明见解析;(2)2.
【解析】
(1)已知AB=AC,BE平分∠ABC,根据等腰三角形三线合一的性质可得BE⊥AC,所以∠ABE+∠A=90°,再由∠ACD+∠A=90°,根据同角的余角相等可得∠ABE=∠ACD,利用ASA判定△BDF≌△CDA,根据全等三角形的性质即可证得BF=AC;(2)如图,过点F作FG⊥BC于点G, 根据角平分线的性质定理可得FD=FG,由△BDF≌△CDA即可得DF=AD=![]() =FG,已知CD⊥BD,CD=BD,根据等腰三角形的性质可得∠DCB=45°,即可求得CF=2 .
=FG,已知CD⊥BD,CD=BD,根据等腰三角形的性质可得∠DCB=45°,即可求得CF=2 .
(1)∵AB=AC,BE平分∠ABC
∴BE⊥AC
∴∠ABE+∠A=90°
∵CD⊥AB
∴∠ACD+∠A=90°
∴∠ABE=∠ACD
∵∠ADC=∠BDF=90°,BD=CD
∴△BDF≌△CDA(ASA)
∴BF=AC
(2)如图,过点F作FG⊥BC于点G, 则FD=FG .
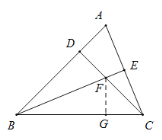
∵△BDF≌△CDA
∴DF=AD=![]() =FG
=FG
∵CD⊥BD,CD=BD
∴∠DCB=45°
∴CF=2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目