题目内容
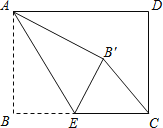
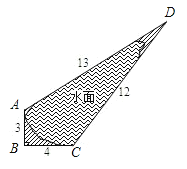
【题目】如图,某风景区的沿湖公路AB=3千米,BC=4千米,CD=12千米,AD=13千米,其中AB^BC,图中阴影是草地,其余是水面.那么乘游艇游点C出发,行进速度为每小时11![]() 千米,到达对岸AD最少要用 小时.
千米,到达对岸AD最少要用 小时.
【答案】0.4
【解析】
连接AC,在直角△ABC中,已知AB,BC可以求AC,根据AC,CD,AD的长度符合勾股定理确定AC⊥CD,则可计算△ACD的面积,又因为△ACD的面积可以根据AD边和AD边上的高求得,故根据△ACD的面积可以求得C到AD的最短距离,即△ACD中AD边上的高.
解:连接AC,
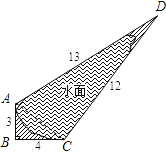
在直角△ABC中,AB=3km,BC=4km,则AC=![]() =5km,
=5km,
∵CD=12km,AD=13km,故存在AD2=AC2+CD2
∴△ACD为直角三角形,且∠ACD=90°,
∴△ACD的面积为![]() ×AC×CD=30km2,
×AC×CD=30km2,
∵AD=13km,∴AD边上的高,即C到AD的最短距离为![]() km,
km,
游艇的速度为11![]() km/小时,
km/小时,
需要时间为![]() 小时=0.4小时.
小时=0.4小时.
故答案为 0.4.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目