题目内容
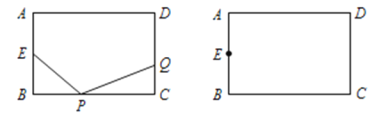
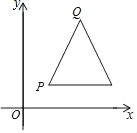
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若PQ为某个等腰三角形的腰,且该等腰三角形的底边与x轴平行,则称该等腰三角形为点P,Q的“相关等腰三角形”.下图为点P,Q的“相关等腰三角形”的示意图.
(1)已知点A的坐标为(0,1),点B的坐标为(-![]() ,0),则点A,B的“相关等腰三角形”的顶角为 °;
,0),则点A,B的“相关等腰三角形”的顶角为 °;
(2)若点C的坐标为(0,![]() ),点D在直线y=4
),点D在直线y=4![]() 上,且C,D的“相关等腰三角形”为等边三角形,求直线CD的表达式;
上,且C,D的“相关等腰三角形”为等边三角形,求直线CD的表达式;
(3)⊙O的半径为![]() ,点N在双曲线y=﹣
,点N在双曲线y=﹣![]() 上.若在⊙O上存在一点M,使得点M、N的“相关等腰三角形”为直角三角形,直接写出点N的横坐标xN的取值范围.
上.若在⊙O上存在一点M,使得点M、N的“相关等腰三角形”为直角三角形,直接写出点N的横坐标xN的取值范围.
【答案】(1)120°;(2)y=![]() x+
x+![]() ,或y=﹣
,或y=﹣![]() x+
x+![]() .(3)﹣3≤xN≤﹣1或1≤xN≤3.
.(3)﹣3≤xN≤﹣1或1≤xN≤3.
【解析】
(1)画出图形求出∠BAO的度数即可解决问题;
(2)利用等边三角形的性质求出点D坐标即可解决问题;
(3)因为点M、N的“相关等腰三角形”为直角三角形,推出直线MN与x轴的夹角为45°,可以假设直线MN的解析式为y=﹣x+b,当直线与⊙O相切于点M时,求出直线MN的解析式,利用方程组求出点N的坐标,观察图象即可解决问题.
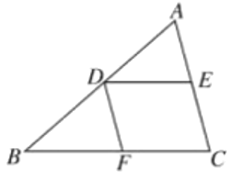
解:(1)如图1中,
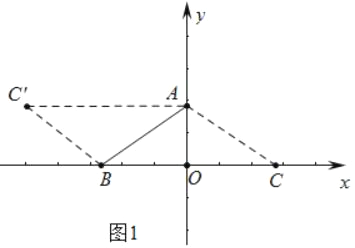
∵A的坐标为(0,1),点B的坐标为![]() ,
,
∴点A,B的“相关等腰三角形”△ABC的当C(![]() ,0)或(﹣2
,0)或(﹣2![]() ,1),
,1),
∵tan∠BAO=![]() =
=![]() ,
,
∴∠BAO=∠CAO=60°,
∴∠BAC=∠ABC′=120°,
故答案为120.
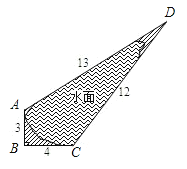
(2)如图2中,设直线y=4![]() 交y轴于F(0,4
交y轴于F(0,4![]() ),
),
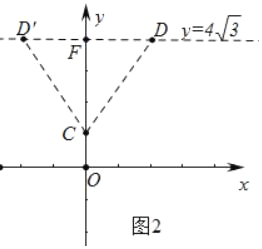
∵C(0,![]() ),
),
∴CF=3![]() ,
,
∵且C,D的“相关等腰三角形”为等边三角形,
∴∠CDF=∠CD′F=60°,
∴DF=FD′=3![]() tan30°=3,
tan30°=3,
∴D(3,4![]() ),D′(﹣3,4
),D′(﹣3,4![]() ),
),
∴直线CD的解析式为y=![]() x+
x+![]() ,或y=﹣
,或y=﹣![]() x+
x+![]() .
.
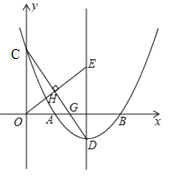
(3)如图3中,
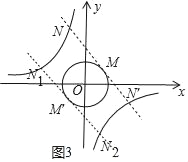
∵点M、N的“相关等腰三角形”为直角三角形,
∴直线MN与x轴的夹角为45°,
可以假设直线MN的解析式为y=﹣x+b,
当直线与⊙O相切于点M时,易知b=±2,
∴直线MN的解析式为y=﹣x+2或y=﹣x﹣2,
由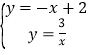 ,解得
,解得![]() 或
或![]() ,
,
∴N(﹣1,3),N′(3,1),
由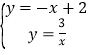 解得
解得![]() 或
或![]() ,
,
∴N1(﹣3,1),N2(1,﹣3),
观察图象可知满足条件的点N的横坐标的取值范围为:﹣3≤xN≤﹣1或1≤xN≤3.

 阅读快车系列答案
阅读快车系列答案【题目】某移动通信公司推出了如下两种移动电话计费方式.
月使用费/元 | 主叫限定时间/分钟 | 主叫超时费(元/分钟) | |
方式一 |
|
|
|
方式二 |
|
|
|
说明:月使用费固定收取,主叫不超过限定时间不再收费,超过部分加收超时费.例如,方式一每月固定交费![]() 元,当主叫计时不超过
元,当主叫计时不超过![]() 分钟不再额外收费,超过
分钟不再额外收费,超过![]() 分钟时,超过部分每分钟加收
分钟时,超过部分每分钟加收![]() 元(不足
元(不足![]() 分钟按
分钟按![]() 分钟计算).
分钟计算).
(1)请根据题意完成如表的填空:
月主叫时间 | 月主叫时间 | |
方式一收费/元 | ______________ |
|
方式二收费/元 |
| _______________ |
(2)设某月主叫时间为![]() (分钟),方式一、方式二两种计费方式的费用分别为
(分钟),方式一、方式二两种计费方式的费用分别为![]() (元),
(元),![]() (元),分别写出两种计费方式中主叫时间
(元),分别写出两种计费方式中主叫时间![]() (分钟)与费用为
(分钟)与费用为![]() (元),
(元),![]() (元)的函数关系式;
(元)的函数关系式;
(3)请计算说明选择哪种计费方式更省钱.