题目内容
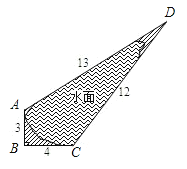
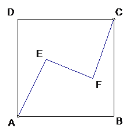
【题目】如图，正方形ABCD内有两点E、F满足AE=FC= 4，EF =6，AE⊥EF，CF⊥EF，则正方形ABCD的面积为 ( )
A.24B.25C.48D.50
【答案】D
【解析】
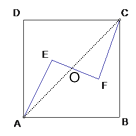
连接AC交EF于O，首先证明△AOE≌△COF，求出OE=OF=3，然后利用勾股定理求出OC，进而得到AC，再利用勾股定理求出AB2即可.
解：如图，连接AC交EF于O，
∵AE=FC= 4，AE⊥EF，CF⊥EF，∠AOE＝∠COF，
∴∠E＝∠F＝90°，
∴△AOE≌△COF（AAS），
∴OE=OF，
∵EF=6，
∴OE=OF=3，
∴
，
∴AC=2OC=10，
∵AB2+BC2=AC2，AB=BC，
∴2AB2=100，
∴AB2=50，即正方形ABCD的面积为50，
故选：D.
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
