题目内容
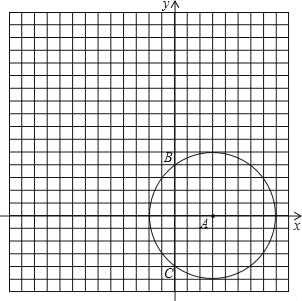
【题目】如图,正方形网格中,每个小正方形的边长为1个单位,以O为原点建立平面直角坐标系,圆心为 A(3,0)的⊙A被y轴截得的弦长BC=8.
解答下列问题:
(1)求⊙A 的半径;
(2)请在图中将⊙A 先向上平移 6 个单位,再向左平移8个单位得到⊙D,并写出圆心D的坐标;
(3)观察你所画的图形,对⊙D 与⊙A 的位置关系作出合情的猜想,并直接写出你的结论.
【答案】(1)⊙A的半径是5;(2)图详见解析,圆心D的坐标是(﹣5,6);(3)⊙D 与⊙A 的位置关系是外切.
【解析】
(1)连接AB,根据垂径定理求出BO,根据勾股定理求出AB即可;
(2)根据已知画出图形即可,根据平移规律求出D的坐标即可;
(3)根据图形即可得出结论.
(1)解:∵x轴⊥y轴,A在x轴上,
∴BO=CO=4,
连接AB,由勾股定理得:AB=![]() =5,
=5,
答:⊙A的半径是5.
(2)解:如图:
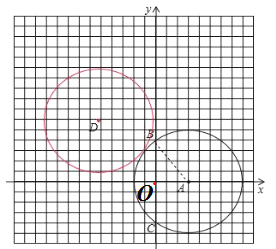
圆心D的坐标是(﹣5,6).
(3)解:⊙D 与⊙A 的位置关系是外切.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目