题目内容
【题目】有一个如图所示的长方体的透明鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点A处沿缸壁爬到鱼缸内G处吃鱼饵.
(1)小虫应该走怎样的路线才可使爬行的路程最短?请画出它的爬行路线,并用箭头标注;
(2)试求小虫爬行的最短路程.
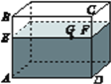
【答案】(1)如图所示见解析,AQ→QG为最短路线;(2)小虫爬行的最短路程为100 cm.
【解析】
(1)根据轴对称性质,通过作对称点将折线转化成两点之间线段距离最短.
(2)根据AE=40cm,AA′=120cm,可得:A′E=120-40=80(cm),再根据EG=60cm,可得:A′G2=A′E2+EG2=802+602=10000,A′G=100cm,进而可得:AQ+QG=A′Q+QG=A′G=100cm.
(1)如图所示,AQ→QG为最短路线,

(2)因为AE=40cm,AA′=120cm,所以A′E=120-40=80(cm),
因为EG=60cm,所以A′G2=A′E2+EG2=802+602=10000,
所以A′G=100cm,所以AQ+QG=A′Q+QG=A′G=100cm,
所以小虫爬行的最短路程为100cm.

练习册系列答案
相关题目