题目内容
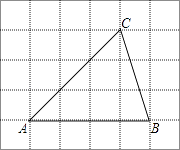
【题目】如图,△ABC中,D是BC上的一点,AB=10,BD=6,AD=8,AC=17.
(1)判断AD与BC的位置关系,并说明理由;
(2)求△ABC的面积.

【答案】(1)AD⊥BC.理由见解析; (2) 84.
【解析】
(1)根据AB=10,BD=6,AD=8,可得BD2+AD2=AB2,根据勾股定理的逆定理可进行判定△ABD是直角三角形,即∠ADB=90°,
(2) 在Rt△ACD中,根据CD2=AC2-AD2=172-82=152,可得CD=15,进而可得S△ABC=![]() BC·AD=
BC·AD=![]() (BD+CD)·AD=
(BD+CD)·AD=![]() ×21×8=84
×21×8=84
(1)AD⊥BC.理由如下:
因为BD2+AD2=62+82=102=AB2,
所以△ABD是直角三角形,且∠ADB=90°,
所以AD⊥BC.
(2)在Rt△ACD中,因为CD2=AC2-AD2=172-82=152,所以CD=15,
所以S△ABC=![]() BC·AD=
BC·AD=![]() (BD+CD)·AD=
(BD+CD)·AD=![]() ×21×8=84.
×21×8=84.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目