题目内容
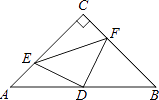
【题目】如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD点于点F. 
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
【答案】
(1)证明:∵ABCD是正方形
∴AD=BC,∠ADC=∠BCD=90°
又∵三角形CDE是等边三角形
∴CE=DE,∠EDC=∠ECD=60°
∴∠ADE=∠ECB
∴△ADE≌△BCE.
(2)解:∵△CDE是等边三角形,
∴CE=CD=DE,
∵四边形ABCD是正方形
∴CD=BC,
∴CE=BC,
∴△CBE为等腰三角形,且顶角∠ECB=90°﹣60°=30°
∴∠EBC= ![]() (180°﹣30°)=75°
(180°﹣30°)=75°
∵AD∥BC
∴∠AFB=∠EBC=75°.
【解析】(1)由题意正方形ABCD的边AD=DC,在等边三角形CDE中,CE=DE,∠EDC等于∠ECD,即能证其全等.(2)根据等边三角形、等腰三角形、平行线的角度关系,可以求得∠AFB的度数.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 阅读快车系列答案
阅读快车系列答案【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人