题目内容
【题目】问题探究:
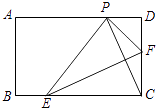
(1)已知:如图1,在正方形ABCD中,点E、H分别在BC、AB上,若AE⊥DH于点O,求证AE=DH;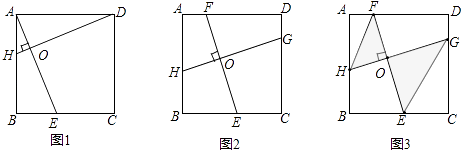
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
拓展应用:
(3)已知,如图3,在(2)问条件下,若BC=4,E为BC的中点,AF= ![]() AD,求HG的长
AD,求HG的长
【答案】
(1)
证明:∵四边形ABCD是正方形,
∴AB=DA,∠ABE=90°=∠DAH.
∴∠HAO+∠OAD=90°.
∵AE⊥DH,
∴∠ADO+∠OAD=90°.
∴∠HAO=∠ADO,
在△ABE和△DAH中
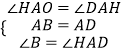 ,
,
∴△ABE≌△DAH(ASA),
∴AE=DH.
(2)
解:EF=GH.
理由:如图2,将FE平移到AM处,则AM∥EF,AM=EF.
将GH平移到DN处,则DN∥GH,DN=GH.
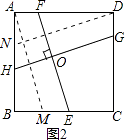
∵EF⊥GH,
∴AM⊥DN,
根据(1)的结论得AM=DN,
所以EF=GH;
(3)
解:如图3,
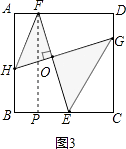
过点F作FP⊥BC于点P,
∵四边形ABCD是正方形,BC=4,
∴AD=BC=AB=FP=4,
∵E为BC的中点,AF= ![]() AD,
AD,
∴BE=2,AF=1,
∴PE=2﹣1=1,
在Rt△FPE中,EF= ![]() =
= ![]() ,
,
由(2)得:HG=EF,
∴HG= ![]() .
.
【解析】(1)由正方形的性质得AB=DA,∠ABE=90°=∠DAH.所以∠HAO+∠OAD=90°,又知∠ADO+∠OAD=90°,所以∠HAO=∠ADO,于是△ABE≌△DAH,可得AE=DH;(2)将FE平移到AM处,则AM∥EF,AM=EF,将GH平移到DN处,则DN∥GH,DN=GH.根据(1)的结论得AM=DN,所以EF=GH;(3)过点F作FP⊥BC于点P,利用勾股定理得出EF的长,进而得出HG的长.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.