题目内容
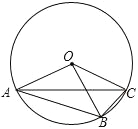
【题目】如图,△ABC中,∠BAC=90°,∠ABC=∠ACB,又∠BDC=∠BCD,且∠1=∠2,求∠3的度数.

【答案】75°
【解析】试题分析:根据已知求得∠ACB=45°,进而求得∠BDC=∠BCD=45°+∠1,根据三角形内角和定理求得2(45°+∠1)+∠1=180°,即可求得∠1=30°,然后根据三角形内角和180°,从而求得∠3的度数.
试题解析:∵∠BAC=90°,∠ABC=∠ACB,
∴∠ACB=45°,
∵∠BDC=∠BCD,∠BCD=∠ACB+∠2,
∴∠BDC=∠BCD=45°+∠2,
∵∠1=∠2,
∴∠BDC=∠BCD=45°+∠1,
∵∠BDC+∠BCD+∠1=180°,
∴2(45°+∠1)+∠1=180°
∴∠1=30°,
∴∠3=![]() =75°.
=75°.

练习册系列答案
相关题目