题目内容
【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线![]() :
:![]() 与
与![]() :
:![]() 为“友好抛物线”.
为“友好抛物线”.
(1)求抛物线![]() 的解析式.
的解析式.
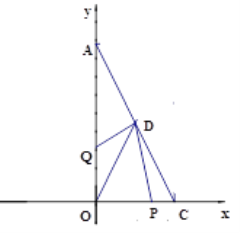
(2)点A是抛物线![]() 上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
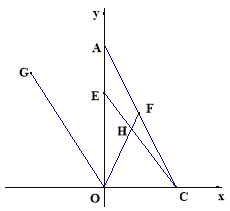
(3)设抛物线![]() 的顶点为C,点B的坐标为(﹣1,4),问在
的顶点为C,点B的坐标为(﹣1,4),问在![]() 的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线
的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线![]() 上?若存在求出点M的坐标,不存在说明理由.
上?若存在求出点M的坐标,不存在说明理由.
【答案】(1) ![]() ;(2) 当a=
;(2) 当a=![]() 时,AQ+OQ有最大值,最大值为
时,AQ+OQ有最大值,最大值为![]() (3)存在点M,(1,2)或(1,5).
(3)存在点M,(1,2)或(1,5).
【解析】
试题分析:(1)先求得![]() 顶点坐标,然后依据两个抛物线的顶点坐标相同可求得m、n的值;
顶点坐标,然后依据两个抛物线的顶点坐标相同可求得m、n的值;
(2)设A(a,![]() ).则OQ=x,AQ=
).则OQ=x,AQ=![]() ,然后得到OQ+AQ与a的函数关系式,最后依据配方法可求得OQ+AQ的最值;
,然后得到OQ+AQ与a的函数关系式,最后依据配方法可求得OQ+AQ的最值;
(3)连接BC,过点B′作B′D⊥CM,垂足为D.接下来证明△BCM≌△MDB′,由全等三角形的性质得到BC=MD,CM=B′D,设点M的坐标为(1,a).则用含a的式子可表示出点B′的坐标,将点B′的坐标代入抛物线的解析式可求得a的值,从而得到点M的坐标.
试题解析:(1)∵![]() =
=![]() ,
,
∴抛物线![]() 的顶点坐标为(1,4).
的顶点坐标为(1,4).
∵抛物线![]() 与
与![]() 顶点相同,
顶点相同,
∴![]() =1,﹣1+m+n=4.
=1,﹣1+m+n=4.
解得:m=2,n=3.
∴抛物线![]() 的解析式为
的解析式为![]() ;
;
(2)如图1所示:

设点A的坐标为(a,![]() ).
).
∵AQ=![]() ,OQ=a,
,OQ=a,
∴AQ+OQ=![]() +a=
+a=![]() =
=![]() .
.
∴当a=![]() 时,AQ+OQ有最大值,最大值为
时,AQ+OQ有最大值,最大值为![]() .
.
(3)存在点M,理由如下:
如图2所示;连接BC,过点B′作B′D⊥CM,垂足为D.

∵B(﹣1,4),C(1,4),抛物线的对称轴为x=1,
∴BC⊥CM,BC=2.
∵∠BMB′=90°,
∴∠BMC+∠B′MD=90°.
∵B′D⊥MC,
∴∠MB′D+∠B′MD=90°.
∴∠MB′D=∠BMC.
在△BCM和△MDB′中,∠MB′D=∠BMC ,∠BCM=∠MDB′,BM=MB′,
∴△BCM≌△MDB′.
∴BC=MD,CM=B′D.
设点M的坐标为(1,a).则B′D=CM=4﹣a,MD=CB=2.
∴点B′的坐标为(a﹣3,a﹣2).
∴![]() ,
,
整理得:![]() ﹣7a+10=0.
﹣7a+10=0.
解得a=2,或a=5.
当a=2时,M的坐标为(1,2),
当a=5时,M的坐标为(1,5).
综上所述当点M的坐标为(1,2)或(1,5)时,B′恰好落在抛物线![]() 上.
上.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.