题目内容
【题目】已知反比例函数y= ![]() (a为常数)的图象经过点B(﹣4,2).
(a为常数)的图象经过点B(﹣4,2).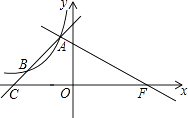
(1)求a的值;
(2)如图,过点B作直线AB与函数y= ![]() 的图象交于点A,与x轴交于点C,且AB=3BC,过点A作直线AF⊥AB,交x轴于点F,求线段AF的长.
的图象交于点A,与x轴交于点C,且AB=3BC,过点A作直线AF⊥AB,交x轴于点F,求线段AF的长.
【答案】
(1)
解:∵图象过点B(﹣4,2),代入y= ![]() ,
,
∴2= ![]() ,
,
解得:a=﹣12
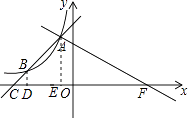
(2)
解:∵a=﹣12,
∴反比例函数解析式为 ![]() ,
,
分别过点A、B作x轴的垂线,垂足分别为点D、E,
∵AB=3BC,
∴ ![]() ,BD=2,
,BD=2,
∵AD∥BE,
∴△BCD∽△ACE,
∴ ![]() ,
,
即 ![]() ,
,
∴AE=8.
∴把y=8代入 ![]() ,
,
得x=﹣1.
∴A(﹣1,8),
设直线AB解析式为y=kx+b,
把A(﹣1,8),B(﹣4,2)代入解析式得, ![]() ,
,
解得: ![]() ,
,
∴直线AB解析式为y=2x+10,
当y=0时,2x+10=0,
解得:x=﹣5,
∴C(﹣5,0),
∴ ![]() ,
,
∵AF⊥AB,AE⊥CF,
∴△ACE∽△FAE,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:AF=8 ![]() .
.
【解析】(1)由反比例函数y= ![]() (a为常数)的图象经过点B(﹣4,2),直接利用待定系数法求解即可求得答案;(2)首先分别过点A、B作x轴的垂线,垂足分别为点D、E,易得△BCD∽△ACE,即可求得A的坐标,由△ACE∽△FAE,即可求得答案.
(a为常数)的图象经过点B(﹣4,2),直接利用待定系数法求解即可求得答案;(2)首先分别过点A、B作x轴的垂线,垂足分别为点D、E,易得△BCD∽△ACE,即可求得A的坐标,由△ACE∽△FAE,即可求得答案.
【考点精析】本题主要考查了反比例函数的概念和反比例函数的图象的相关知识点,需要掌握形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点才能正确解答此题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目