题目内容
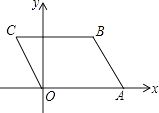
【题目】如图，在平面直角坐标系xOy中，一次函数y=k1x+b与反比例函数y= 
的图象交于点A（﹣3，2）和点B（1，m），连接BO并延长与反比例函数y= 的图象交于点C． 
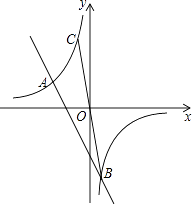
（1）求一次函数y=k1x+b和反比例函数y= 的表达式；
（2）是否在双曲线y= 上存在一点D，使得以点A、B、D、C为顶点的四边形成为平行四边形？若存在，请直接写出点D的坐标，并求出该平行四边形的面积；若不存在，请说明理由．
【答案】
（1）解：将A（﹣3，2）代入反比例解析式得：k2=﹣6，
则反比例解析式为y=﹣ 
；
将B（1，m）代入反比例解析式得：m=﹣6，即B（1，﹣6），
将A与B坐标代入y=k1x+b中，得： 
，
解得： 
，
则一次函数解析式为y=﹣2x﹣4；
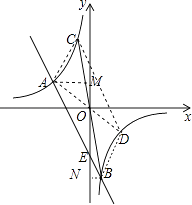
（2）解：存在，
∵B、C关于原点对称，B（1，﹣6），
∴C（﹣1，6），
∵四边形ABDC是平行四边形，
∴CD∥AB，
∴设直线CD的解析式为y=﹣2x+n，
代入C（﹣1，6）得，6=2+n，
解得n=4，
解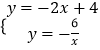 
得 
或 
，
∴D（3，﹣2）；
作AM⊥y轴于M，BN⊥y轴于N，设直线AB交y轴于E，则E（0，﹣4），
∴OE=4，
∴S△AOB=S△AOE+S△BOE= 
OEAM+ OEBN
= ×4×3+ ×4×1=8，
∴S平行四边形=4S=4×8=32
【解析】（1）将A坐标代入反比例解析式求出k2的值，确定出反比例解析式，将B坐标代入反比例解析式求m的值，确定出B坐标，将A与B坐标代入一次函数解析式求出k1与b的值，即可确定出一次函数解析式；（2）根据中心对称求得C的坐标，然后根据平移的性质和A、C、B的坐标即可求得D的坐标，作AM⊥y轴于M，BN⊥y轴于N，设直线AB交y轴于E，则E（0，﹣4），根据S△AOB=S△AOE+S△BOE求得△AOB的面积，进而即可求得平行四边形的面积．
