题目内容
实践操作
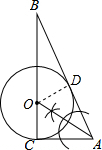
如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)作∠BAC的平分线,交BC于点O;
(2)以O为圆心,OC为半径作圆.
综合运用
在你所作的图中,
(1)AB与⊙O的位置关系是______;(直接写出答案)
(2)若AC=5,BC=12,求⊙O的半径.

如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)作∠BAC的平分线,交BC于点O;
(2)以O为圆心,OC为半径作圆.
综合运用
在你所作的图中,
(1)AB与⊙O的位置关系是______;(直接写出答案)
(2)若AC=5,BC=12,求⊙O的半径.

实践操作,如图所示:
综合运用:
(1)AB与⊙O的位置关系是相切.
∵AO是∠BAC的平分线,
∴DO=CO,
∵∠ACB=90°,
∴∠ADO=90°,
∴AB与⊙O的位置关系是相切;
(2)∵AC=5,BC=12,
∴AD=5,AB=
=13,
∴DB=AB-AD=13-5=8,
设半径为x,则OC=OD=x,BO=(12-x)
x2+82=(12-x)2,
解得:x=
.
答:⊙O的半径为
.
综合运用:
(1)AB与⊙O的位置关系是相切.
∵AO是∠BAC的平分线,
∴DO=CO,
∵∠ACB=90°,
∴∠ADO=90°,
∴AB与⊙O的位置关系是相切;
(2)∵AC=5,BC=12,
∴AD=5,AB=
| 52+122 |
∴DB=AB-AD=13-5=8,
设半径为x,则OC=OD=x,BO=(12-x)
x2+82=(12-x)2,
解得:x=
| 10 |
| 3 |
答:⊙O的半径为
| 10 |
| 3 |


练习册系列答案
相关题目