Question

【题目】如图1，AB是⊙O的直径，E是AB延长线上一点，EC切⊙O于点C，OP⊥AO交AC于点P，交EC的延长线于点D．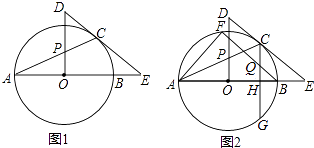

（1）求证：△PCD是等腰三角形；
（2）CG⊥AB于H点，交⊙O于G点，过B点作BF∥EC，交⊙O于点F，交CG于Q点，连接AF，如图2，若sinE= ，CQ=5，求AF的值．

Answer 1

【答案】
（1）解：连接OC，

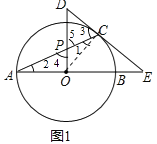
∵EC切⊙O于点C，

∴OC⊥DE，

∴∠1+∠3=90°，

又∵OP⊥OA，

∴∠2+∠4=90°，

∵OA=OC，

∴∠1=∠2，

∴∠3=∠4，

又∵∠4=∠5，

∴∠3=∠5，

∴DP=DC，即△PCD为等腰三角形

（2）解：如图2，连接OC、BC，

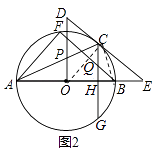
∵DE与⊙O相切于点E，

∴∠OCB+∠BCE=90°，

∵OC=OB，

∴∠OCB=∠OBC，

∴∠OBC+∠BCE=90°，

又∵CG⊥AB，

∴∠OBC+∠BCG=90°，

∴∠BCE=∠BCG，

∵BF∥DE，

∴∠BCE=∠QBC，

∴∠BCG=∠QBC，

∴QC=QB=5，

∵BF∥DE，

∴∠ABF=∠E，

∵sinE= ，

∴sin∠ABF= ，

∴QH=3、BH=4，

设⊙O的半径为r，

∴在△OCH中，r2=82+（r﹣4）2，

解得：r=10，

又∵∠AFB=90°，sin∠ABF= ，

∴AF=12．

【解析】本题主要考查切线的性质、平行线的性质及三角函数的应用等知识的综合，根据切线性质和平行线性质及垂直性质证∠BCG=∠QBC是解题的关键．（1）连接OC，由切线性质和垂直性质得∠1+∠3=90°、∠2+∠4=90°，继而可得∠3=∠5得证；（2）连接OC、BC，先根据切线性质和平行线性质及垂直性质证∠BCG=∠QBC得QC=QB=5，而sinE=sin∠ABF= ，可知QH=3、BH=4，设圆的半径为r，在RT在△OCH中根据勾股定理可得r的值，在RT△ABF中根据三角函数可得答案．