Question

【题目】如图，已知点A的坐标为（﹣2，0），直线y=﹣ x+3与x轴、y轴分别交于点B和点C，连接AC，顶点为D的抛物线y=ax2+bx+c过A、B、C三点．

（1）请直接写出B、C两点的坐标，抛物线的解析式及顶点D的坐标；
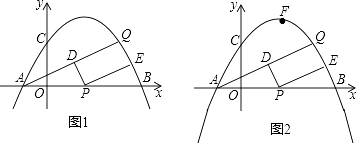
（2）设抛物线的对称轴DE交线段BC于点E，P是第一象限内抛物线上一点，过点P作x轴的垂线，交线段BC于点F，若四边形DEFP为平行四边形，求点P的坐标；
（3）设点M是线段BC上的一动点，过点M作MN∥AB，交AC于点N，点Q从点B出发，以每秒1个单位长度的速度沿线段BA向点A运动，运动时间为t（秒），当t（秒）为何值时，存在△QMN为等腰直角三角形？

Answer 1

【答案】
（1）

解：令x=0代入y=﹣ x+3

∴y=3，

∴C（0，3），

令y=0代入y=﹣ x+3

∴x=4，

∴B（4，0），

设抛物线的解析式为：y=a（x+2）（x﹣4），

把C（0，3）代入y=a（x+2）（x﹣4），

∴a=﹣ ，

∴抛物线的解析式为：y= （x+2）（x﹣4）=﹣ x2+ x+3，

∴顶点D的坐标为（1， ）；

（2）

解：当DP∥BC时，

此时四边形DEFP是平行四边形，

设直线DP的解析式为y=mx+n，

∵直线BC的解析式为：y=﹣ x+3，

∴m=﹣ ，

∴y=﹣ x+n，

把D（1， ）代入y=﹣ x+n，

∴n= ，

∴直线DP的解析式为y=﹣ x+ ，

∴联立 ，

解得：x=3或x=1（舍去），

∴把x=3代入y=﹣ x+ ，

y= ，

∴P的坐标为（3， ）；

（3）

解：由题意可知：0≤t≤6，

设直线AC的解析式为：y=m1x+n1，

把A（﹣2，0）和C（0，3）代入y=m1x+n1，

得： ，∴解得 ，

∴直线AC的解析式为：y= x+3，

由题意知：QB=t，

如图1，当∠NMQ=90°，

∴OQ=4﹣t，

令x=4﹣t代入y=﹣ x+3，

∴y= t，

∴M（4﹣t， t），

∵MN∥x轴，

∴N的纵坐标为 t，

把y= t代入y= x+3，

∴x= t﹣2，

∴N（ t﹣2， t），

∴MN=（4﹣t）﹣（ ﹣2）=6﹣ t，

∵MQ∥OC，

∴△BQM∽△BOC，

∴ ，

∴MQ= t，

当MN=MQ时，

∴6﹣ t= t，

∴t= ，

此时QB= ，符合题意，

如图2，当∠QNM=90°时，

∵QB=t，

∴点Q的坐标为（4﹣t，0）

∴令x=4﹣t代入y= x+3，

∴y=9﹣ t，

∴N（4﹣t，9﹣ t），

∵MN∥x轴，

∴点M的纵坐标为9﹣ t，

∴令y=9﹣ t代入y=﹣ x+3，

∴x=2t﹣8，

∴M（2t﹣8，9﹣ t），

∴MN=（2t﹣8）﹣（4﹣t）=3t﹣12，

∵NQ∥OC，

∴△AQN∽△AOC，

∴ = ，

∴NQ=9﹣ t，

当NQ=MN时，

∴9﹣ t=3t﹣12，

∴t= ，

∴此时QB= ，符合题意

如图3，当∠NQM=90°，

过点Q作QE⊥MN于点E，

过点M作MF⊥x轴于点F，

设QE=a，

令y=a代入y=﹣ x+3，

∴x=4﹣ ，

∴M（4﹣ a，a），

令y=a代入y= x+3，

∴x= ﹣2，

∴N（ ﹣2，a），

∴MN=（4﹣ a）﹣（ a﹣2）=6﹣2a，

当MN=2QE时，

∴6﹣2a=2a，

∴a= ，

∴MF=QE= ，

∵MF∥OC，

∴△BMF∽△BCO，

∴ = ，

∴BF=2，

∴QB=QF+BF= +2= ，

∴t= ，此情况符合题意，

综上所述，当△QMN为等腰直角三角形时，此时t= 或 或 ．

【解析】（1）分别令y=0和x=0代入y=﹣ x+3即可求出B和C的坐标，然后设抛物线的交点式为y=a（x+2）（x﹣4），最后把C的坐标代入抛物线解析式即可求出a的值和顶点D的坐标；（2）若四边形DEFP为平行四边形时，则DP∥BC，设直线DP的解析式为y=mx+n，则m=﹣ ，求出直线DP的解析式后，联立抛物线解析式和直线DP的解析式即可求出P的坐标；（3）由题意可知，0≤t≤6，若△QMN为等腰直角三角形，则共有三种情况，①∠NMQ=90°；②∠MNQ=90°；③∠NQM=90°．
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．