题目内容
【题目】在△ABC中,∠ACB=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D,E,F是垂足,且AB=5,BC=4,AC=3,则点O到三边AB,AC,BC的距离分别是( )
A. 1,1,1 B. 2,2,2 C. 1,1.5,2 D. 无法确定
【答案】A
【解析】
由角平分线的性质易得OE=OF=OD,AE=AF,CE=CD,BD=BF,设OE=OF=OD=x,则CE=CD=x,BD=BF=4-x,AF=AE=3-x,所以3-x+4-x=5,解答即可.
连接OB,如图所示:
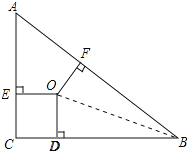
∵点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,
∴OE=OF=OD,
在△BOF与△BOD中,
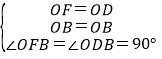 ,
,
∴Rt△BOF≌Rt△BOD(HL),
∴BD=BF,
同理可证:AE=AF,CE=CD,
∵∠C=90°,OD⊥BC,OE⊥AC,OF⊥AB,OD=OE,
∴OECD是正方形,
设OE=OF=OD=x,则CE=CD=x,BD=BF=4-x,AF=AE=3-x,
∴BF+FA=AB=5,即3-x+4-x=5,
解得x=1,
则OE=OF=OD=1,
故选A.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目