题目内容
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点B在原点O,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3, ![]() ),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是 .
),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是 . 
【答案】(2,0)或(4,0)
【解析】解:①如图1中,当∠AFE=90°,
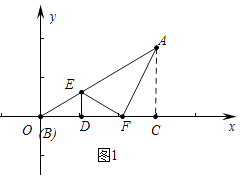
∵A(3, ![]() ),
),
∴OC=3,AC= ![]() ,
,
∴tan∠AOC= ![]() =
= ![]() ,
,
∴∠AOC=30°,
∵EO=EF,
∴∠EOF=∠EFO=30°,
∴∠AEF=∠EOF+∠EFO=60°,
∴∠EAF=∠FAC=30°,
∴CF=ACtan30°=1,
∴OF=OC﹣CF=2,
∴F(2,0).
②如图2中,当∠EAF=90°时,
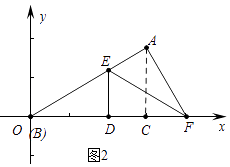
易知∠CAF=30°,
CF=ACtan30°=1,
∴OF=OC+CF=4,
∴F(4,0),
③∠AEF=60°,不可能为90°.
所以答案是:(2,0)或(4,0).
【考点精析】解答此题的关键在于理解锐角三角函数的定义的相关知识,掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数,以及对特殊角的三角函数值的理解,了解分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.

练习册系列答案
相关题目