Question

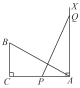
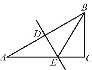
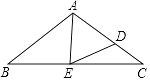
【题目】如图，在等腰△ABC中，AB=AC，点D在AC边上，点E在BC边上，且∠AED=∠B，若AB=10，BE=5，AE=2 ，则线段CE的长为（ ）
A.
B.8
C.2
D.9

Answer 1

【答案】B
【解析】解：∵AB=AC，

∴∠B=∠C，

∵∠AED=∠B，

∴∠AED=∠C，

∵∠EAD=∠CAE，

∴△ACE∽△AED，

∴ ，即 ，

∴AD=6，

∴CD=4，

∵∠B=∠C=∠AED，

∴∠BAE=180°﹣∠B﹣∠AEB，∠DEC=180°﹣∠AEB﹣∠AED，

∴∠BAE=∠DEC，

∴△ABE∽△ECD，

∴ ，即 = ，

∴CE=8．

故选B．

【考点精析】通过灵活运用等腰三角形的性质和相似三角形的判定与性质，掌握等腰三角形的两个底角相等（简称：等边对等角）；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．