Question

【题目】将一块直角三角板放置在锐角上，使得该三角板的两条直角边恰好分别经过点

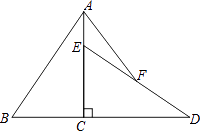
（1）如图①，若时，点在内，则 度，____度， 度；

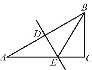
（2）如图②，改变直角三角板的位置，使点在内，请探究与之间存在怎样的数量关系，并验证你的结论；

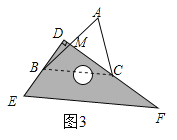
（3）如图③，改变直角三角板的位置，使点在外，且在边的左侧，直接写出三者之间存在的数量关系．

Answer 1

【答案】（1）135；90；45；（2）∠ABD+∠ACD=90°-∠A，证明见解析；（3）∠ACD-∠ABD=90°-∠A

【解析】

（1）在△BCD中，根据三角形内角和定理可得∠DBC+∠DCB =90°，在△ABC中，根据三角形内角和定理可得∠ABC+∠ACB=135°，进而可求出∠ABD+∠ACD的度数；

（2）根据三角形内角和定理可得∠ABC+∠ACB=180°-∠A，∠DBC+∠DCB=90°，

整理可得∠ABD+∠ACD=90°-∠A；

（3）根据三角形内角和定理可得∠ACD+∠A+∠AMC=180°，∠ABD+∠D+∠BMD=180°，整理可得∠ACD-∠ABD=90°-∠A．

解：（1）在△ABC中，∵∠A=45°，

∴∠ABC+∠ACB=180°-45°=135°，

在△DBC中，∵∠BDC=90°，

∴∠DBC+∠DCB=180°-90°=90°，

∴∠ABD+∠ACD=135°-90°=45°；

故答案为：135；90；45．

（2）∠ABD+∠ACD与∠A之间的数量关系为：∠ABD+∠ACD=90°-∠A．证明如下：

在△ABC中，∠ABC+∠ACB=180°-∠A．

在△DBC中，∠DBC+∠DCB=90°．

∴∠ABC+∠ACB-(∠DBC+∠DCB)=180°-∠A-90°．

∴∠ABD+∠ACD=90°-∠A．

（3）∠ACD-∠ABD=90°-∠A．

如图③，设AB交CD于点M，

∵∠ACD+∠A+∠AMC=180°，∠ABD+∠D+∠BMD=180°，∠AMC=∠BMD，

∴∠ACD-∠ABD=90°-∠A．