题目内容
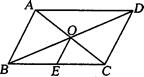
如图,□ABCD中,过点B作BG∥AC,在BG上取一点E,连结DE交AC的延长线于点F.

(1)求证:DF=EF;
(2)如果AD=2,∠ADC=60°,AC⊥DC于点C,AC=2CF,求BE的长.

(1)求证:DF=EF;
(2)如果AD=2,∠ADC=60°,AC⊥DC于点C,AC=2CF,求BE的长.
(1)连结BD交AC于点O,根据平行四边形的性质可得OB=OD,再根据等分线段成比例的性质求解即可;(2)

试题分析:(1)连结BD交AC于点O,根据平行四边形的性质可得OB=OD,再根据等分线段成比例的性质求解即可;
(2)由AC⊥DC,AD=2,∠ADC=60°可得AC=
 ,由OF是△DBE的中位线可得BE=2OF,即可得到BE=2OC+2CF,再根据平行四边形的性质求解即可.
,由OF是△DBE的中位线可得BE=2OF,即可得到BE=2OC+2CF,再根据平行四边形的性质求解即可.(1)连结BD交AC于点O

∵四边形ABCD是平行四边形
∴OB=OD
∵BG∥AC
∴DF=EF;
(2)∵AC⊥DC,AD=2,∠ADC=60°,
∴AC=

∵OF是△DBE的中位线
∴BE="2OF"
∵OF=OC+CF
∴BE=2OC+2CF
∵四边形ABCD是平行四边形
∴AC=2OC,
∵AC=2CF
∴BE=2AC=
 .
.点评:平行四边形的判定与性质是初中数学的重点,贯穿于整个初中数学的学习,是中考常见题,一般难度不大,需熟练掌握.

练习册系列答案
相关题目



 B.
B. C.
C. D.
D.

 cm B.
cm B. cm
cm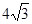 cm D.3 cm
cm D.3 cm