题目内容
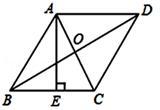
如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E,点F在BD上,连接AF、EF.

(1)求证:DA=DE;
(2)如果AF∥CD,请判断四边形ADEF是什么特殊的四边形,并证明您的结论.

(1)求证:DA=DE;
(2)如果AF∥CD,请判断四边形ADEF是什么特殊的四边形,并证明您的结论.
(1)△BDA全等于△BDE,即可;(2)菱形
试题分析:
1.∵AD∥BC∴∠ADB=∠CBD
∵BC=CD∴∠CDB=∠CBD∴∠ADB=∠EDB
又BD=BD∴Rt△ADB≌Rt△EDB∴AD=ED
2.∵AF∥CD∴∠AFD=∠EDF=∠ADF
∴AF=AD=ED 又∵AF∥ED∴四边形ADEF是平行四边形
又∵AD=ED∴四边形ADEF是菱形
点评:本题难度中等,主要考查学生对四边形性质知识点的掌握,注意培养数形结合思想的掌握,运用到考试中去。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答: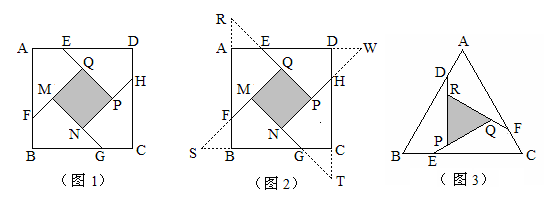
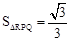 ,则AD的长为 。
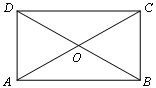
,则AD的长为 。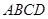 的对角线
的对角线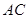 、
、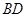 的长分别为
的长分别为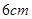 、
、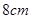 ,
,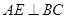 于点
于点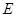 ,则
,则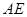 的长是
的长是 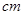 .
.

 ,过
,过 上到点
上到点 的距离分别为:
的距离分别为: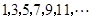 的点作
的点作 相交,得到并标出一组黑色梯形,它们的面积分别为
相交,得到并标出一组黑色梯形,它们的面积分别为 .观察图中的规律,第n(n为正整数)个黑色梯形的面积
.观察图中的规律,第n(n为正整数)个黑色梯形的面积 .
.
