题目内容
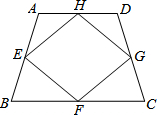
如图,在等腰梯形ABCD中,AD∥BC,E,F,G,H分别是梯形各边的中点.
(1)请用全等符号表示出图中所有的全等三角形(不得添加辅助线),并选其中一对加以证明;
(2)求证:四边形EFGH是菱形.
(1)请用全等符号表示出图中所有的全等三角形(不得添加辅助线),并选其中一对加以证明;
(2)求证:四边形EFGH是菱形.

证明:(1)∵在等腰梯形ABCD中,AD∥BC,
∴∠A=∠D,AB=CD,
∵E,F,G,H分别是梯形各边的中点,
∴AH=DH,AE=DG,
在△AEH和△DGH中,
,
∴△AEH≌△DGH(SAS),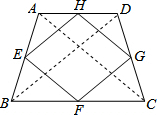
同理可得:△BEF≌△CGF.
∴图中所有的全等三角形有:△AEH≌△DGH,△BEF≌△CGF;
(2)连接AC,BD,
∵梯形ABCD是等腰梯形,
∴AC=BD,
∵E,F,G,H分别是梯形各边的中点,
∴EH=FG=
BD,GH=EF=
AC,
∴EH=GH=GF=EF,
∴四边形EFGH是菱形.
∴∠A=∠D,AB=CD,
∵E,F,G,H分别是梯形各边的中点,
∴AH=DH,AE=DG,
在△AEH和△DGH中,
|
∴△AEH≌△DGH(SAS),

同理可得:△BEF≌△CGF.
∴图中所有的全等三角形有:△AEH≌△DGH,△BEF≌△CGF;
(2)连接AC,BD,
∵梯形ABCD是等腰梯形,
∴AC=BD,
∵E,F,G,H分别是梯形各边的中点,
∴EH=FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴EH=GH=GF=EF,
∴四边形EFGH是菱形.

练习册系列答案
相关题目
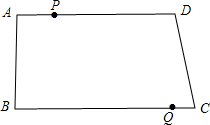 点P、Q分别从A、C同时出发,设运动时间为t(s).
点P、Q分别从A、C同时出发,设运动时间为t(s).