题目内容
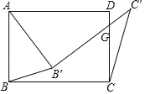
【题目】如图,在正方形![]() 中,点
中,点![]() 是边
是边![]() 上的一点(不与
上的一点(不与![]() 、
、![]() 重合),点
重合),点![]() 在
在![]() 的延长线上,且满足
的延长线上,且满足![]() ,连接
,连接![]() 、
、![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .
.
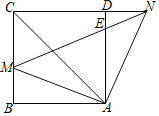
(1)求证:![]() ;
;
(2)如果![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)由正方形的性质得出AB=AD,∠CAD=∠ACB=45°,∠BAD=∠CDA=∠B=90°,然后根据等量代换得出∠BAM=∠DAN,利用ASA可证△ABM≌△ADN,从而利用全等三角形的性质即可证明AM=AN;
(2)根据正方形的性质和![]() 得出∠CAM=∠NAD,∠ACB=∠MNA=45°,从而有△AMC∽△AEN,则
得出∠CAM=∠NAD,∠ACB=∠MNA=45°,从而有△AMC∽△AEN,则![]() =
=![]() ,又因为AN=AM,所以有AN2=AEAC.
,又因为AN=AM,所以有AN2=AEAC.
解:证明(1)∵四边形ABCD是正方形,
∴AB=AD,∠CAD=∠ACB=45°,∠BAD=∠CDA=∠B=90°,
∴∠BAM+∠MAD=90°,∠ADN=90°
∵∠MAN=90°,
∴∠MAD+∠DAN=90°,
∴∠BAM=∠DAN,
且AD=AB,∠ABC=∠ADN=90°
∴△ABM≌△ADN(ASA)
∴AM=AN,
(2)∵AM=AN,∠MAN=90°,
∴∠MNA=45°,
∵∠CAD=2∠NAD=45°,
∴∠NAD=22.5°
∴∠CAM=∠MAN﹣∠CAD﹣∠NAD=22.5°
∴∠CAM=∠NAD,∠ACB=∠MNA=45°,
∴△AMC∽△AEN
∴![]() =
=![]() ,且AN=AM,
,且AN=AM,
∴AN2=AEAC

【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
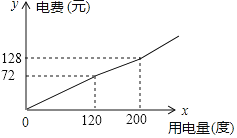
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?