题目内容
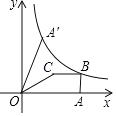
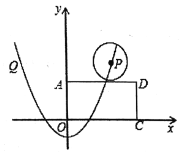
【题目】如图，平面坐标内，矩形
的顶点
、
、
，抛物线
经过点
，
，
的半径为1，当圆心
在抛物线上从点运动到点
，则在整个运动过程中，与矩形只有一个公共点的情况共出现______次．
【答案】3
【解析】
先利用抛物线的解析式求出P,Q的坐标，然后分析P点的运动过程，从中找到
与矩形
只有一个公共点的情况即可．
∵
∴令
解得
∴
令
解得
∴抛物线顶点坐标为
，与坐标轴两交点为
当P开始运动到刚与AD边接触时，此时与矩形只有一个公共点；
当P继续向下运动始终与矩形有两个公共点，直到P运动到抛物线顶点（0，-1）结束；
当P运动到抛物线的顶点时，此时与矩形只有一个公共点；
当P点继续向上运动，直到运动到
时，此时与矩形只有一个公共点；
之后P再继续向Q点运动，不会与矩形产生公共点
所以整个过程中出现了3次
故答案为：3．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
【题目】某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为8.1元/斤，并且两次降价的百分率相同．
（1）求该种水果每次降价的百分率；
（2）从第一次降价的第1天算起，第x天（x为整数）的售价、销量及储存和损耗费用的相关信息如表所示：
时间x（天） | 1≤x≤7 | 8≤x≤14 |
售价（元/斤） | 第1次降价后的价格 | 第2次降价后的价格 |
销量（斤） | 80﹣3x | 120﹣x |
储存和损耗费用（元） | 40+3x | 3x2﹣64x+400 |
已知该种水果的进价为4.1元/斤，设销售该水果第x（天）的利润为y（元），求y与x（1≤x≤14）之间的函数关系式，并求出第几天时销售利润最大？
