题目内容
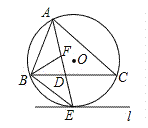
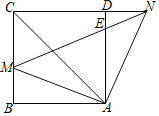
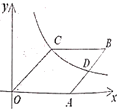
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .作
.作![]() 于
于![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() (
(![]() ),解答下列问题:
),解答下列问题:
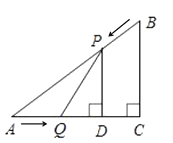
(1)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最大值;
的最大值;
(2)当![]() 的值为________________时,
的值为________________时,![]() 是等腰三角形
是等腰三角形
【答案】(1)![]() (
(![]() ),
),![]() 时,
时,![]() 有最大值是
有最大值是![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据题意,判定![]() ,得出
,得出![]() ,得出AQ、PD含有
,得出AQ、PD含有![]() 的式子,利用面积即可列出函数关系式,然后化为顶点式,即可求出最大值;
的式子,利用面积即可列出函数关系式,然后化为顶点式,即可求出最大值;
(2)分三种情况求解:①当AP=AQ时,②当AQ=QP时,③当![]() 时,由(1)中得知AP、AQ、PQ含有
时,由(1)中得知AP、AQ、PQ含有![]() 的式子,格局勾股定理构建一元二次方程,即可得解.
的式子,格局勾股定理构建一元二次方程,即可得解.
(1)![]()
![]()
又![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
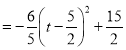
![]() ,
,
![]() 时,
时,![]() 有最大值是
有最大值是![]() ;
;
(2)![]() 或
或![]() 或
或![]()
由(1)中得,![]() ,
,
![]() ,即
,即![]() ,
,![]()
∴![]()
∴
①当AP=AQ时,即![]()
![]() ;
;
②当AQ=QP时,即![]()
![]() 或
或![]() (舍去)
(舍去)
∴![]() ;
;
③当![]() 时,即
时,即![]()
![]() 或
或![]() (舍去)
(舍去)
∴![]() ;
;
综上,![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
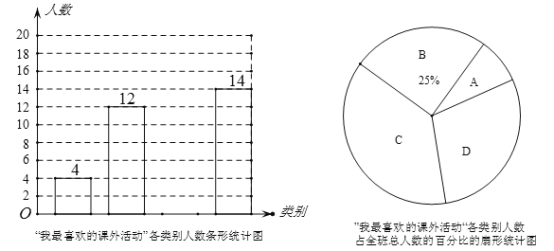
【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图

根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.