题目内容
【题目】已知点O为直线AB上的一点,∠BOC=∠DOE=90°
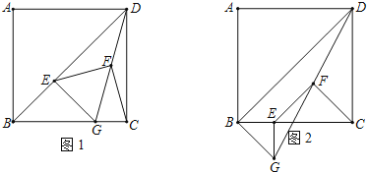
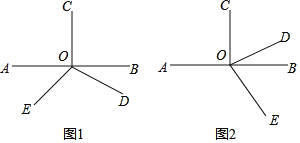
(1)如图1,当射线OC、射线OD在直线AB的两侧时,请回答结论并说明理由;
①∠COD和∠BOE相等吗?
②∠BOD和∠COE有什么关系?
(2)如图2,当射线OC、射线OD在直线AB的同侧时,请直接回答;
①∠COD和∠BOE相等吗?
②第(1)题中的∠BOD和∠COE的关系还成立吗?
【答案】(1)①∠COD=∠BOE,理由见解析;②∠BOD+∠COE=180°,理由见解析;(2)①∠COD=∠BOE,②成立
【解析】
(1)①根据等式的性质,在直角的基础上都加∠BOD,因此相等,②将∠BOD+∠COE转化为两个直角的和,进而得出结论;
(2)①根据同角的余角相等,可得结论,②仍然可以将∠BOD+∠COE转化为两个直角的和,得出结论.
解:(1)①∠COD=∠BOE,理由如下:
∵∠BOC=∠DOE=90°,
∴∠BOC+∠BOD=∠DOE+∠BOD,
即∠COD=∠BOE,
②∠BOD+∠COE=180°,理由如下:
∵∠DOE=90°,∠AOE+∠DOE+∠BOD=∠AOB=180°,
∴∠BOD+∠AOE=180°﹣90°=90°,
∴∠BOD+∠COE=∠BOD+∠AOE+∠AOC=90°+90°=180°,
(2)①∠COD=∠BOE,
∵∠COD+∠BOD=∠BOC=90°=∠DOE=∠BOD+∠BOE,
∴∠COD=∠BOE,
②∠BOD+∠COE=180°,
∵∠DOE=90°=∠BOC,
∴∠COD+∠BOD=∠BOE+∠BOD=90°,
∴∠BOD+∠COE=∠BOD+∠COD+∠BOE+∠BOD=∠BOC+∠DOE=90°+90°=180°,
因此(1)中的∠BOD和∠COE的关系仍成立.

练习册系列答案
相关题目