Question

【题目】在△ABC中，∠B=90°∠A

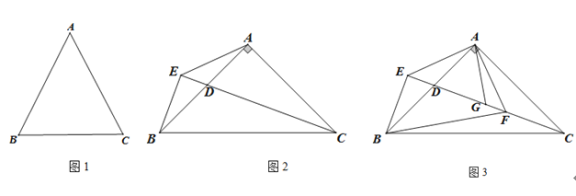
(1)如图1，求证：AB=AC；

(2)如图2，若∠BAC=90°，点D为AB上一点，过点B作直线CD的垂线，垂足为E，连接AE， 求∠AEC的度数；

(3)如图3，在(2)的条件下，过点A作AE的垂线交CE于点F，连接BF，若∠ABF-∠EAB=15°，G为DF上一点，连接AG，若∠AGD=∠EBF，AG=6,求CF的长.

Answer 1

【答案】（1）证明见详解；（2）45°；（3）6

【解析】

（1）利用三角形内角和定理求出，即可证明，即可证明AB=AC；

（2）在CE上截取CF=BE，连接AF,通过证明,可得证明是等腰直角三角形，从而求出∠AEC；

（3）由（2）得出，证明，得出，利用角的转换求出∠AGD=∠EBF=60°，再根据30°直角三角形的性质求出EF，然后再根据勾股定理求出CF的长度.

解：（1）=

=90°∠A

∴

∴AB=AC

（2）如图：

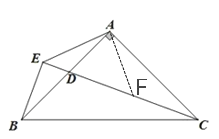
在CE上截取CF=BE，连接AF

由（1）得AB=AC

∴

又∠BAC=90°，（对顶角）

∴

在和中

∴

∴AE=AF,

又∠BAC=∠DAF+∠FAC=90°

∴∠DAF+∠EAB=90°

∴EAF是等腰直角三角形

∴∠AEC=45°

（3）如图：作AHEC

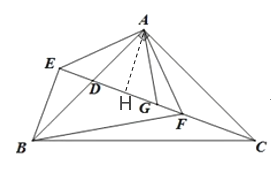
由（2）得

（对顶角相等）

又∠ABF-∠EAB=15°

∴∠AGD=∠EBF=60°

∴在RtAHG中，HG=

∴EF=

在RtBEF中 ，设BE=x,则BF=2x

∴

解得：

∴BE=6

∴CF=BE=6