题目内容
【题目】李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题，请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.
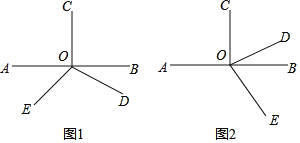
(1) 如图1，正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处；
(2) 如图2，有一圆柱形食品盒，它的高等于16cm，底面直径为20cm.如果在盒外底面的边缘A处有一只蚂蚁，它想吃到盒外对面中点B处的食物；(盒的厚度和蚂蚁的大小忽略不计，结果可含π)
(3) 如图3, 有一无盖的圆柱形食品盒，它的高等于16cm，底面直径为20cm.如果在盒外底面的边缘A处有一只蚂蚁，它想吃到盒内对面中点B处的食物.(盒的厚度和蚂蚁的大小忽略不计，结果可含π)
【答案】（1）
cm；（2）
；（3）
.
【解析】
（1）将长方体侧面展开，直接利用勾股定理得出AC1的长，进而得出答案；
（2）将圆柱侧面展开，首先求出AC的长，再利用勾股定理求出AB的长；
（3）将圆柱侧面展开，再将内部展开，首先求出AC的长，再利用勾股定理求出AB′的长．
(1)如图，将长方体侧面展开，
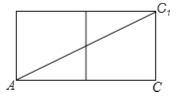
易得AC=5×2=10 cm.CC1=5cm.
在Rt△ACC1中，由勾股定理，得
答：蚂蚁需要爬行的最短路程的长为cm.
（2）如图，将圆柱体侧面展开，
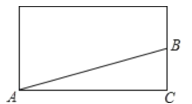
AC=2πR=2π×10÷2=10π cm，
BC=16÷2=8cm.
故
=
=
答：蚂蚁需要爬行的最短路程的长；
（3）如图，将圆柱体侧面展开，再将内部展开
AC=2πR=2π×10÷2=10π cm，
BC=16÷2+16=24cm.
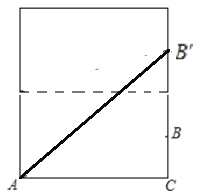
在Rt△AB′C中，由勾股定理，得
故蚂蚁需要爬行的最短路程的长.
练习册系列答案
相关题目
