题目内容
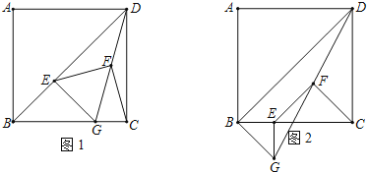
【题目】如图1,在正方形![]() 中,
中,![]() 是对角线,点
是对角线,点![]() 在
在![]() 上,
上,![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,点
,点![]() 是
是![]() 的中点,连结
的中点,连结![]() 与
与![]() .
.
(1)求证:![]() .
.
(2)求证:![]() .
.
(3)如图2,若等腰直角三角形![]() 绕点
绕点![]() 按顺时针旋转
按顺时针旋转![]() ,其他条件不变,请判断
,其他条件不变,请判断![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
【答案】(1)证明见解析;(2)证明见解析;(3)△CEF是等腰直角三角形.
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半,可得EF=DF=![]() DG,CF=DF=
DG,CF=DF=![]() DG,从而得到结论;
DG,从而得到结论;
(2)根据等边对等角可得![]() 再根据三角形的一个外角等于和它不相邻的两个内角和求出
再根据三角形的一个外角等于和它不相邻的两个内角和求出![]() 然后根据正方形的对角线平分一组对角求出
然后根据正方形的对角线平分一组对角求出![]() ,求出
,求出![]() ,从而得证;
,从而得证;
(3)延长![]() 交
交![]() 于
于![]() ,先求出
,先求出![]() ,再根据两直线平行,内错角相等,求出
,再根据两直线平行,内错角相等,求出![]() ,然后利用ASA证明
,然后利用ASA证明![]() 和
和![]() 全等,根据全等三角形对应边相等,可得EG=DH,EF=FH,再求出CE=CH,然后根据等腰三角形三线合一的性质证明即可.
全等,根据全等三角形对应边相等,可得EG=DH,EF=FH,再求出CE=CH,然后根据等腰三角形三线合一的性质证明即可.
解:(1)证明:![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
![]() ,
,
∵正方形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ;
;
(2)证明:![]() ,
,
![]() ,
,
![]()
![]() ,
,
在正方形![]() 中,
中,![]() ,
,
![]() ,
,
![]() ;
;
(3)解:![]() 是等腰直角三角形.
是等腰直角三角形.
理由如下:如图,延长![]() 交
交![]() 于
于![]() ,
,
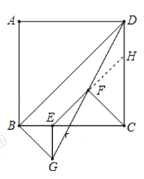
∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() (等腰三角形三线合一),
(等腰三角形三线合一),![]() ,
,
∴△CEF是等腰直角三角形.

练习册系列答案
相关题目
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去……
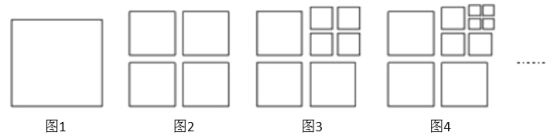
(1)根据图中的规律补全下表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
| n |
正方形个数 | 1 | 4 | 7 | 10 |
|
(2)求第几幅图形中有2020个正方形?