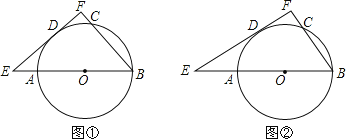题目内容
【题目】如图1,在三角形![]() 中,
中,![]() ,
,![]() 和
和![]() 关于
关于![]() 对称
对称
(1)将图1中的![]() 以
以![]() 为旋转中心,逆时针方向旋转角
为旋转中心,逆时针方向旋转角![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,分别延长
,分别延长![]() 和
和![]() 交于点
交于点![]() ,则四边形
,则四边形![]() 的形状是 ;
的形状是 ;
(2)将图1中的![]() 以
以![]() 为旋转中心,按逆时针方向旋转角
为旋转中心,按逆时针方向旋转角![]() ,使
,使![]() ,得到如图3所示的
,得到如图3所示的![]() ,连接
,连接![]() 和
和![]() ,得到四边形
,得到四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图3中,![]() ,将
,将![]() 沿着射线
沿着射线![]() 方向平移
方向平移![]() ,得到
,得到![]() ,连接
,连接![]() ,使四边形
,使四边形![]() 恰好为正方形,请直接写出a的值.
恰好为正方形,请直接写出a的值.

【答案】(1)菱形;(2)四边形BCC′D是矩形,理由见解析;(3)a的值为![]() 或
或![]() .
.
【解析】
(1)由对称的性质结合题意得出DC=BC=DA=AB,∠BAC=∠DAC=∠BCA=∠DCA,由旋转的性质得出∠CAC′=∠BAC=∠AC′D=∠BCA,证出AC∥DE,AC′∥BE,得出四边形ACEC′是平行四边形,由旋转可得:AC=AC′,即可得出四边形ACEC′是菱形;
(2)过点A作AE⊥C′C于点E,由旋转的性质,得AC′=AC,得出∠CAE=∠C′AE=![]() α=∠BAC,∠AEC′=90°,由等腰三角形的性质得出∠BCA=∠BAC,进而得出∠CAE=∠BCA,证出AE∥BC.同理,AE∥DC′,得出BC∥DC′,证出四边形BCC′D是平行四边形,求出∠BCC'=90°,即可得出四边形BCC′D是矩形;
α=∠BAC,∠AEC′=90°,由等腰三角形的性质得出∠BCA=∠BAC,进而得出∠CAE=∠BCA,证出AE∥BC.同理,AE∥DC′,得出BC∥DC′,证出四边形BCC′D是平行四边形,求出∠BCC'=90°,即可得出四边形BCC′D是矩形;
(3)过点B作BF⊥AC于F,证明△ACE∽△CBF,得出![]() ,求出CE=
,求出CE=![]() ,由等腰三角形的性质得出CC′=2CE=
,由等腰三角形的性质得出CC′=2CE=![]() ,当四边形BCC′'D′恰好为正方形时,分两种情况:①C′'在边CC′上时,a=CC′CC';②当点C′'在C′C的延长线上时,a=CC′+CC'.
,当四边形BCC′'D′恰好为正方形时,分两种情况:①C′'在边CC′上时,a=CC′CC';②当点C′'在C′C的延长线上时,a=CC′+CC'.
解:(1)∵△ADC和△ABC关于AC对称,
∴DC=BC,DA=AB,∠BAC=∠DAC,∠BCA=∠DCA,
∵BA=BC,
∴DC=BC=DA=AB,∠BAC=∠DAC=∠BCA=∠DCA,
∵△ACD以A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到△AC′D,
∴∠CAC′=∠BAC=∠AC′D=∠BCA,
∴AC∥DE,AC′∥BE,
∴四边形ACEC′是平行四边形,
由旋转可得:AC=AC′,
∴四边形ACEC′是菱形,
故答案为:菱形;
(2)四边形BCC′D是矩形;
理由:过点A作AE⊥C′C于点E,如图3所示:

由旋转的性质,得AC′=AC,
∴∠CAE=∠C′AE=![]() α=∠BAC,∠AEC′=90°,
α=∠BAC,∠AEC′=90°,
∵BA=BC,
∴∠BCA=∠BAC,
∴∠CAE=∠BCA,
∴AE∥BC,
同理,AE∥DC′,
∴BC∥DC′,
∵BC=DC′,
∴四边形BCC′D是平行四边形,
∵AE∥BC,∠AEC′=90°,
∴∠BCC′=90°,
∴四边形BCC′D是矩形;
(3)过点B作BF⊥AC于F,
∵BA=BC,
∴CF=AF![]() AC=
AC=![]() ×10=5,
×10=5,
在Rt△BCF中,BF=![]() ,
,
∵∠CAE=∠BCF,∠CEA=∠BFC=90°,
∴△ACE∽△CBF,
∴![]() ,即
,即![]() ,
,
解得:CE=![]() ,
,
∵AC=AC′,AE⊥CC′,
∴CC′=2CE=![]() ,
,
当四边形BCC′'D′恰好为正方形时,CC'=BC=![]() ,
,
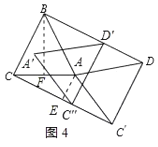
分两种情况:①C′'在边CC′上时,如图4所示:
则a=CC′CC'=![]() ;
;
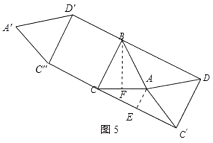
②当点C′'在C′C的延长线上时,如图5所示:
则a=CC′+CC'=![]() ;
;
综上所述,a的值为![]() 或
或![]() .
.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
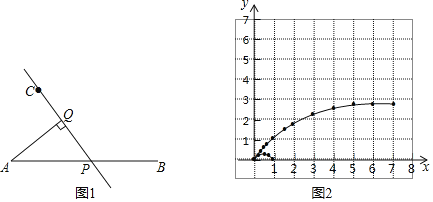
芒果教辅暑假天地重庆出版社系列答案【题目】如图1,线段AB及一定点C、P是线段AB上一动点,作直线CP,过点A作AQ⊥CP于点Q,已知AB=7cm,设A、P两点间的距离为xcm,A、Q两点间的距离为y1cm,P、Q两点间的距离为y2cm.小明根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值.
x/cm | 0 | 0.3 | 0.5 | 0.8 | 1 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 |
y1/cm | 0 | 0.28 | 0.49 | 0.79 | 1 | 1.48 | 1.87 | 2.37 | 2.61 | 2.72 | 2.76 | 2.78 |
y2/cm | 0 | 0.08 | 0.09 | 0.06 | 0 | 0.29 | 0.73 | 1.82 |
| 4.20 | 5.33 | 6.41 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(3)结合函数图象,解决问题:当△APQ中有一个角为30°时,AP的长度约为 cm.