题目内容
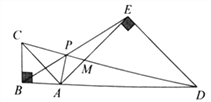
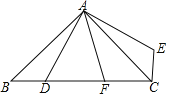
【题目】已知,AB为⊙O的直径,C,D为⊙O上两点,过点D的直线EF与⊙O相切,分别交BA,BC的延长线于点E,F,BF⊥EF
(I)如图①,若∠ABC=50°,求∠DBC的大小;
(Ⅱ)如图②,若BC=2,AB=4,求DE的长.
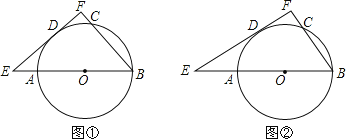
【答案】(1)25°;(2)2![]() .
.
【解析】
(1)如图1,连接OD,BD,由EF与⊙O相切,得到OD⊥EF,由于BF⊥EF,得到OD∥BF,得到∠AOD=∠ABC=50°,由外角的性质得到结果;
(2)如图2,连接AC,OD,根据AB为⊙O的直径,得出∠ACB=90°,由直角三角形的性质得到∠CAB=30°,于是AC=ABcos30°=4×![]() =2
=2![]() ,AH=AOcos30°=2×
,AH=AOcos30°=2×![]() =
=![]() ,根据三角形的中位线的性质解得结果.
,根据三角形的中位线的性质解得结果.
解(1)如图1,连接OD,BD,
∵EF与⊙O相切,
∴OD⊥EF,
∵BF⊥EF,
∴OD∥BF,
∴∠AOD=∠ABC=50°,
∵OD=OB,
∴∠OBD=∠ODB=![]() ∠AOD=25°
∠AOD=25°
∴∠DBC=∠OBC-∠OBD=25°;
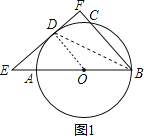
(2)如图2,连接AC,OD,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC=2,AB=4,
∴∠CAB=30°,
∴AC=ABcos30°=4×![]() =2
=2![]() ,
,
∵∠ODF=∠F=∠HCO=90°,
∴∠DHC=90°,
∴AH=AOcos30°=2×![]() =
=![]() ,
,
∵∠HAO=30°,
∴OH=![]() OA=
OA=![]() OD,
OD,
∵AC∥EF,
∴DE=2AH=2![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】2019年中国北京世界园艺博览会已于2019年4月29日在北京市延庆区开展,吸引了大批游客参观游览.五一小长假期间平均每天入园人数大约是8万人,佳佳等5名同学组成的学习小组,随机调查了五一假期中入园参观的部分游客,获得了他们在园内参观所用时间,并对数据进行整理,描述和分析,下面给出了部分信息:
a.参观时间的频数分布表如下:
时间 | 频数(人数) | 频率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合计 |
| 1.000 |
b.参观时间的频数分布直方图如图:
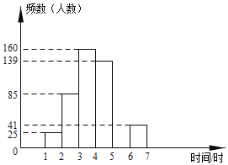
根据以上图表提供的信息,解答下列问题:
(1)这里采用的调查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并请补全频数分布直方图;
(4)请你估算五一假期中平均每天参观时间小于4小时的游客约有多少万人?