题目内容
【题目】抛物线y=﹣x2+bx+c(b,c为常数)与x轴交于点(x1,0)和(x2,0),与y轴交于点A,点E为抛物线顶点.
(Ⅰ)当x1=﹣1,x2=3时,求点E,点A的坐标;
(Ⅱ)①若顶点E在直线y=x上时,用含有b的代数式表示c;
②在①的前提下,当点A的位置最高时,求抛物线的解析式;
(Ⅲ)若x1=﹣1,b>0,当P(1,0)满足PA+PE值最小时,求b的值.
【答案】(Ⅰ)点A的坐标为(0,3),点E的坐标为(1,4);(Ⅱ)①c=![]() ;②
;②![]() ;(Ⅲ)3+
;(Ⅲ)3+![]() .
.
【解析】
(Ⅰ)根据题意和x1=﹣1,x2=3,可以得到点(﹣1,0),(3,0)在抛物线y=﹣x2+bx+c的图象上,然后即可求得该抛物线的解析式,再将抛物线解析式化为顶点式,即可得到点A和点E的坐标;
(Ⅱ)①将题目中的函数解析式化为顶点式,再根据题目中顶点E在直线y=x上,即可得到c和b的关系;
②根据①的结果和二次函数的性质,可以求得当点A的位置最高时,抛物线的解析式;
(Ⅲ)根据x1=﹣1,b>0和题目中的函数解析式,可以得到点A的坐标,然后即可求得直线AP的解析式,再根据最短路线问题可以得到当P(1,0)满足PA+PE值最小时b的值.
解:(Ⅰ)∵抛物线y=﹣x2+bx+c(b,c为常数)与x轴交于点(x1,0)和(x2,0),与y轴交于点A,点E为抛物线顶点,x1=﹣1,x2=3,
∴点(﹣1,0),(3,0)在抛物线y=﹣x2+bx+c的图象上,
∴![]() ,解得
,解得![]() ,
,
∴y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴点A的坐标为(0,3),点E的坐标为(1,4);
(Ⅱ)①∵y=﹣x2+bx+c=![]() ,
,
∴点E的坐标为(![]() ,
,![]() ),
),
∵顶点E在直线y=x上,
∴![]() =
=![]() ,
,
∴c=![]() ;
;
②由①知,![]() ,
,
则点A的坐标为(0,![]() ),
),
∴当b=1时,此时点A的位置最高,函数y=﹣x2+x+![]() ,
,
即在①的前提下,当点A的位置最高时,抛物线的解析式是![]() ;
;
(Ⅲ)∵x1=﹣1,抛物线y=﹣x2+bx+c过点(x1,0),
∴﹣1﹣b+c=0,
∴c=1+b,
∵点E的坐标为(![]() ,
,![]() ),点A的坐标为(0,c),
),点A的坐标为(0,c),
∴E(![]() ,
,![]() ),A(0,b+1),
),A(0,b+1),
∴点E关于x轴的对称点E′(![]() ,﹣
,﹣![]() ),
),
设过点A(0,b+1)、P(1,0)的直线解析式为y=kx+t,
![]() ,得
,得![]() ,
,
∴直线AP的解析式为y=(﹣b﹣1)x+(b+1)=﹣(b+1)x+(b+1)=(b+1)(﹣x+1),
∵当直线AP过点E′时,PA+PE值最小,
∴﹣![]() =(b+1)(﹣
=(b+1)(﹣![]() +1),
+1),
化简得:b2﹣6b﹣8=0,
解得:b1=![]() ,b2=
,b2=![]()
∵b>0,
∴b=![]() ,
,
即b的值是3+![]() .
.

【题目】2019年中国北京世界园艺博览会已于2019年4月29日在北京市延庆区开展,吸引了大批游客参观游览.五一小长假期间平均每天入园人数大约是8万人,佳佳等5名同学组成的学习小组,随机调查了五一假期中入园参观的部分游客,获得了他们在园内参观所用时间,并对数据进行整理,描述和分析,下面给出了部分信息:
a.参观时间的频数分布表如下:
时间 | 频数(人数) | 频率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合计 |
| 1.000 |
b.参观时间的频数分布直方图如图:
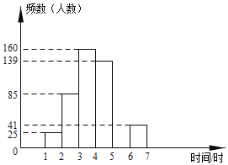
根据以上图表提供的信息,解答下列问题:
(1)这里采用的调查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并请补全频数分布直方图;
(4)请你估算五一假期中平均每天参观时间小于4小时的游客约有多少万人?
【题目】设函数y=k1x+![]() ,且k1k2≠0,自变量x与函数值y满足以下表格:
,且k1k2≠0,自变量x与函数值y满足以下表格:
x | …… | -4 | -3 | -2 | -1 | - |
| 1 | 2 | 3 | 4 | …… |
y | …… | -3 | -2 | -1 | 0 | 1 | -1 | 0 | 1 | m | n | …… |
(1)根据表格直接写出y与x的函数表达式及自变量x的取值范围______
(2)补全上面表格:m=______,n=______;在如图所示的平面直角坐标系中,请根据表格中的数据补全y关于x的函数图象;
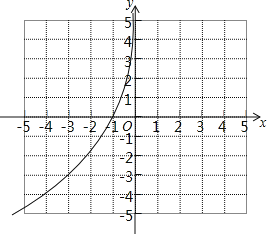
(3)结合函数图象,解决下列问题:
①写出函数y的一条性质:______;
②当函数值y≥![]() 时,x的取值范围是______;
时,x的取值范围是______;
③当函数值y=-x时,结合图象请估算x的值为______(结果保留一位小数)