题目内容
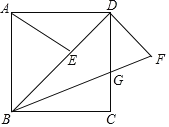
【题目】如图,在正方形ABCD中,点E是对角线BD上一点,连接AE,将DE绕D点逆时针方向旋转90°到DF,连接BF,交DC于点G,若DG=3,CG=2,则线段AE的长为__.
【答案】![]() .
.
【解析】
连接EF,过点E作EM⊥AD,垂足为M,设ME=HE=FH=x,则GH=3-x,从而可得到![]() ,于是可求得x的值,最后在Rt△AME中,依据勾股定理可求得AE的长.
,于是可求得x的值,最后在Rt△AME中,依据勾股定理可求得AE的长.
如图所示:连接EF,过点E作EM⊥AD,垂足为M.
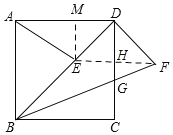
∵ABCD为正方形,EM⊥AD,∠EDF=90°,
∴△MED和△DEF均为等腰直角三角形.
∵DE=DF,∠EDH=∠FDH=45°,
∴DH⊥EF,EH=HF,
∴FH∥BC.
设ME=HE=FH=x,则GH=3﹣x.
由FH∥BC可知:![]() ,
,
即![]() ,解得:
,解得:![]() ,
,
∴![]() .
.
在Rt△AME中,![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目