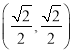Question

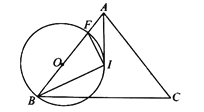
【题目】如图，在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，以CD为直径的⊙O分别交AC、BC于点M、N，过点N作NE⊥AB，垂足为E．

（1）若⊙O的半径为，AC＝6，求BN的长；

（2）求证：NE与⊙O相切．

Answer 1

【答案】（1）4；（2）见解析

【解析】

（1）由直角三角形斜边上的中点到三顶点距离相等，得BD＝CD，又由直径所对的圆周角是直角得DN⊥BC，由三线合一知BN＝NC，即可求得答案；

（2）证明切线，一般先把圆心和切点连接，然后证明垂直，由(1)知，通过角的转化，即可证明ON⊥NE，从而证得结论.

（1）连接DN，ON

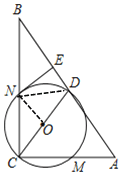
∵⊙O的半径为，

∴CD＝5

∵∠ACB＝90°，CD是斜边AB上的中线，

∴BD＝CD＝AD＝5，

∴AB＝10，

∴

∵CD为直径

∴∠CND＝90°，即DN⊥BC，且BD＝CD

∴BN＝NC＝4

（2）∵∠ACB＝90°，D为斜边的中点，

∴，

∴∠BCD＝∠B，

∵OC＝ON，

∴∠BCD＝∠ONC，

∴∠ONC＝∠B，

∴ON∥AB，

∵NE⊥AB，

∴ON⊥NE，

∴NE为⊙O的切线．