题目内容
【题目】如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA. 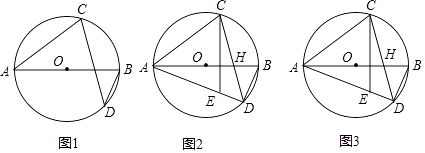
(1)求证:∠ABD=2∠BDC;
(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
【答案】
(1)解:如图1,设∠BDC=α,∠DAC=β,
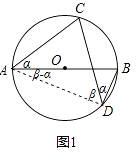
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,
∴ ![]() =
= ![]() ,
,
∴∠ADC=∠DAC=β,
∴∠DAB=β﹣α,
连接AD,
∵AB为⊙O直径,
∴∠ADB=90°,
∴α+β=90°,
∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),
∴∠ABD=2α,
∴∠ABD=2∠BDC;
(2)解:∵CE⊥AB,
∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,
∴∠ACE=∠ADC,
∵∠CAE=∠ADC,
∴∠ACE=∠CAE,
∴AE=CE;
(3)解:如图2,连接OC,
∴∠COB=2∠CAB,
∵∠ABD=2∠BEC,∠BDC=∠CAB,
∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,
∴△OCH∽△ABD,
∴ ![]() ,
,
∵OH=5,
∴BD=10,
∴AB= ![]() =26,
=26,
∴AO=13,
∴AH=18,
∵△AHE∽△ADB,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AE= ![]() ,
,
∴DE= ![]() .
.
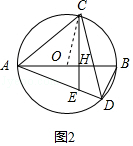
【解析】(1)如图1,设∠BDC=α,∠DAC=β,根据圆周角定理得到∠CAB=∠BDC=α,连接AD,由AB为⊙O直径,得到∠ADB=90°,根据余角的性质即可得到结论;(2)根据已知条件得到∠ACE=∠ADC,等量代换得到∠ACE=∠CAE,于是得到结论;(3)如图2,连接OC,根据圆周角定理得到∠COB=2∠CAB,等量代换得到∠COB=∠ABD,根据相似三角形的性质得到OH=5,根据勾股定理得到AB= ![]() =26,由相似三角形的性质即可得到结论.
=26,由相似三角形的性质即可得到结论.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.